Atsisiųskite iš „Depositfiles“.

4. PAVIRŠIŲ TEORIJA.

4.1 PAVIRŠIAUS LYGTYBĖS.

Paviršius trimatėje erdvėje gali būti nurodytas:

1) netiesiogiai: F ( x , y , z ) =0 (4.1)

2) aiškiai: z = f ( x , y ) (4.2)

3) parametriškai: (4.3)

arba:
(4.3’)

kur skaliariniai argumentai
kartais vadinamos kreivinėmis koordinatėmis. Pavyzdžiui, sfera
patogu nurodyti sferinėmis koordinatėmis:
.

4.2 LIETIMO PLOKŠTUMA IR NORMALI PAVIRŠIAUS.

Jei tiesė yra ant paviršiaus (4.1), tada jos taškų koordinatės tenkina paviršiaus lygtį:

Išskirdami šią tapatybę, gauname:

(4.4)

arba
(4.4 ’ )

kiekviename paviršiaus kreivės taške. Taigi gradiento vektorius nevienaskaitiuose paviršiaus taškuose (kuriuose funkcija (4.5) yra diferencijuojama ir
) yra statmenas bet kurių paviršiaus linijų liestinės vektoriams, t. y. gali būti naudojamas kaip normalusis vektorius liestinės plokštumos lygčiai taške M sudaryti 0 (x 0 , y 0 , z 0 ) paviršius

(4.6)

ir kaip krypties vektorius normaliojoje lygtyje:

(4.7)

Esant aiškiam (4.2) paviršiaus specifikavimui, liestinės plokštumos ir normaliosios lygtys yra atitinkamai tokios formos:

(4.8)

Ir
(4.9)

Su parametriniu paviršiaus vaizdavimu (4.3), vektoriai
yra liestinės plokštumoje, o liestinės plokštumos lygtis gali būti parašyta taip:

(4.10)

ir jų vektoriaus sandauga gali būti laikoma krypties normaliuoju vektoriumi:

ir normalioji lygtis gali būti parašyta taip:

(4.11)

Kur
— parametrų reikšmės, atitinkančios tašką M 0 .

Toliau mes apsiribosime nagrinėdami tik tokius paviršiaus taškus, kuriuose yra vektoriai

nelygu nuliui ir nėra lygiagreti.

4.1 pavyzdys Sukurkite liestinės plokštumos ir normaliosios lygtis taške M 0 (1,1,2) į apsisukimo paraboloido paviršių
.

Sprendimas: Kadangi paraboloidinė lygtis pateikta aiškiai, pagal (4.8) ir (4.9) turime rasti
taške M 0 :

ir taške M 0
. Tada liestinės plokštumos taške M lygtis 0 bus tokia forma:

2(x -1)+2(y -1)-(z-2) = 0 arba 2 x +2 y – z - 2=0, ir normalioji lygtis
.

4.2 pavyzdys Sudarykite liestinės plokštumos ir normaliosios lygtis savavališkame sraigto formos taške
, .

Sprendimas. cia,

Tangentinės plokštumos lygtis:

arba

Normalios lygtys:

.

4.3 PIRMOJI KvadRATINĖ PAVIRŠIAUS FORMA.

Jei paviršius pateikiamas lygtimi

tada kreivė
jį galima pateikti lygtimi
(4.12)

Spindulio vektoriaus diferencialas
išilgai kreivės, atitinkančios poslinkį nuo taško M 0 iki artimiausio taško M, yra lygus

(4.13)

Nes
yra kreivės lanko skirtumas, atitinkantis tą patį poslinkį), tada

(4.14)

Kur.

Dešinėje (4.14) pusėje esanti išraiška vadinama pirmąja kvadratine paviršiaus forma ir vaidina didžiulį vaidmenį paviršių teorijoje.

Integruoju diferencialąds pradedant nuo t 0 (atitinka M tašką 0 ) iki t (atitinka tašką M), gauname atitinkamos kreivės atkarpos ilgį

(4.15)

Žinodami pirmąją kvadratinę paviršiaus formą, galite rasti ne tik ilgius, bet ir kampus tarp kreivių.

Jeigu du , dv yra kreivinių koordinačių skirtumai, atitinkantys be galo mažą poslinkį išilgai vienos kreivės, ir
- kita vertus, atsižvelgiant į (4.13):

(4.16)

Naudojant formulę

(4.17)

pirmoji kvadratinė forma leidžia apskaičiuoti regiono plotą
paviršiai.

4.3 pavyzdys Ant spiralės suraskite spiralės ilgį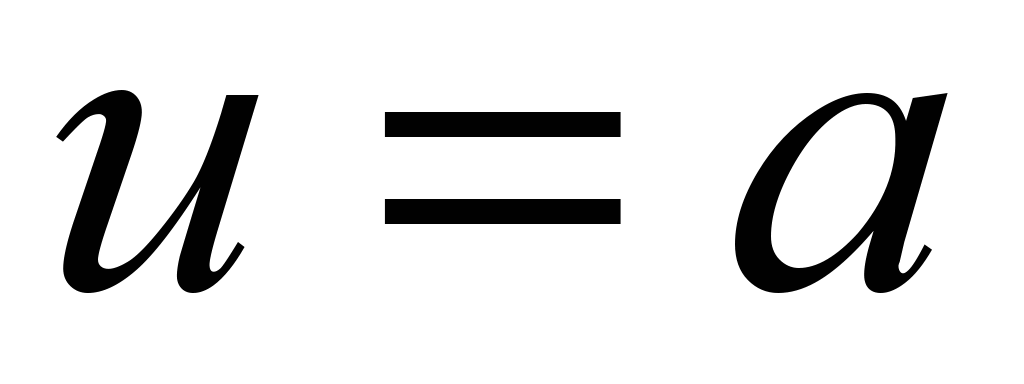
tarp dviejų taškų.

Sprendimas. Nes ant spiralės
, Tai. Raskime taške
pirmoji kvadratinė forma. Paskyrus irv = t , gauname šios sraigtinės linijos lygtį formoje . Kvadratinė forma:

= - pirmoji kvadratinė forma.

čia . Šiuo atveju formulėje (4.15).
ir lanko ilgis:

=

4.4 ANTRA KvadRATINĖ PAVIRŠIAUS FORMA.

Pažymėkime
- vieneto vektorius, normalus paviršiui
:

(4.18) . (4.23)

Paviršiaus linija vadinama kreivumo linija, jei jos kryptis kiekviename taške yra pagrindinė kryptis.

4.6 GEODEZINIŲ LINJŲ ANT PAVIRŠIAUS SAMPRATA.

Apibrėžimas 4.1 . Paviršiaus kreivė vadinama geodezine, jei jos pagrindinė norma kiekviename taške, kur kreivumas yra ne nulis, jis sutampa su normaliu į paviršių.

Per kiekvieną paviršiaus tašką bet kuria kryptimi praeina tik vienas geodezinis. Pavyzdžiui, sferoje didieji apskritimai yra geodezija.

Paviršiaus parametrų nustatymas vadinamas pusiau geodeziniu, jei viena koordinačių linijų šeima susideda iš geodezinių elementų, o antroji yra statmena jai. Pavyzdžiui, sferoje yra dienovidiniai (geodeziniai) ir paralelės.

Pakankamai mažame segmente esanti geodezija yra trumpiausia iš visų šalia jo esančių kreivių, jungiančių tuos pačius taškus.

Normalios plokštumos lygtis

1.

4.

Tangentinė plokštuma ir paviršius normalūs

Tegul koks nors paviršius yra, A yra fiksuotas paviršiaus taškas, o B yra kintamas paviršiaus taškas,

(1 pav.).

Nenulinis vektorius

→

n

paskambino normalus vektoriusį paviršių taške A, jei

lim B → A j = π 2 .

Paviršiaus taškas F (x, y, z) = 0 vadinamas paprastu, jei šiame taške

1. dalinės išvestinės F " x , F " y , F " z yra tolydžios;
2. (F "x)2 + (F"y)2 + (F"z)2 ≠ 0.

Jei pažeidžiama bent viena iš šių sąlygų, vadinamas paviršiaus tašku specialus paviršiaus taškas .

1 teorema. Jei M(x 0 , y 0 , z 0 ) yra paprastasis paviršiaus taškas F (x , y , z) = 0 , tada vektorius

→ n = F laipsnis (x 0 , y 0 , z 0 ) = F " x (x 0 , y 0 , z 0 ) → i + F "y (x 0 , y 0 , z 0 ) → j + F "z (x 0 , y 0 , z 0 ) → k

(1)

yra normalus šiam paviršiui taške M (x 0 , y 0 , z 0 ) .

Įrodymas knygoje pateikta I.M. Petruško, L.A. Kuznecova, V.I. Prokhorenko, V.F. Safonova `` Aukštosios matematikos kursas: Integralinis skaičiavimas. Kelių kintamųjų funkcijos. Diferencialinės lygtys. M.: Leidykla MPEI, 2002 (p. 128).

Normalus paviršiui tam tikrame taške yra tiesė, kurios krypties vektorius yra normalus paviršiui šiame taške ir kuri eina per šį tašką.

Kanoninis normalios lygtys gali būti pavaizduotas formoje

x − x 0 F "x (x 0 , y 0 , z 0 ) = y - y 0 F "y (x 0 , y 0 , z 0 ) = z − z 0 F "z (x 0 , y 0 , z 0 ) .

(2)

Tangentinė plokštumaį paviršių tam tikrame taške yra plokštuma, kuri eina per šį tašką statmena šio taško paviršiaus normaliai.

Iš šio apibrėžimo išplaukia, kad liestinės plokštumos lygtis turi formą:

(3)

Jei paviršiaus taškas yra vienaskaita, tai tame taške paviršiui normalaus vektoriaus gali ir nebūti, todėl paviršius gali neturėti normaliosios ir liestinės plokštumos.

Dviejų kintamųjų funkcijos bendro diferencialo geometrinė reikšmė

Tegul funkcija z = f (x, y) yra diferencijuojama taške a (x 0, y 0). Jo grafikas yra paviršius

f (x, y) − z = 0.

Įdėkime z 0 = f (x 0 , y 0 ) . Tada taškas A (x 0, y 0, z 0) priklauso paviršiui.

Funkcijos F (x, y, z) = f (x, y) − z dalinės išvestinės yra

F " x = f " x , F " y = f " y , F " z = - 1

ir taške A (x 0 , y 0 , z 0 )

1. jie yra ištisiniai;
2. F "2 x + F "2 y + F "2 z = f "2 x + f "2 y + 1 ≠ 0.

Vadinasi, A yra įprastas paviršiaus F (x, y, z) taškas ir šiame taške yra paviršiaus liestinė. Pagal (3) liestinės plokštumos lygtis yra tokia:

f "x (x 0 , y 0 ) (x - x 0 ) + f " y (x 0 , y 0 ) (y - y 0 ) - (z - z 0 ) = 0.

Vertikalus taško poslinkis liestinės plokštumoje, judant iš taško a (x 0, y 0) į savavališką tašką p (x, y), yra B Q (2 pav.). Atitinkamas paraiškų prieaugis yra

(z − z 0 ) = f " x (x 0 , y 0 ) (x - x 0 ) + f " y (x 0 , y 0 ) (y - y 0 )

Čia, dešinėje, yra diferencialas d z funkcija z = f (x, y) taške a (x 0, x 0). Vadinasi,
d f (x 0, y 0). yra liestinės plokštumos taško pritaikymo funkcijos f (x, y) grafikui taške (x 0, y 0, z 0 = f (x 0, y 0)) prieaugis.

Iš diferencialo apibrėžimo matyti, kad atstumas tarp taško P funkcijos grafike ir taško Q liestinės plokštumoje yra aukštesnės eilės begalinis dydis nei atstumas nuo taško p iki taško a.

Liečiamosios plokštumos vaidina didelį vaidmenį geometrijoje. Liečiamųjų plokštumų konstrukcija turi praktinę reikšmę, nes jų buvimas leidžia nustatyti normalios kryptį į paviršių sąlyčio taške. Ši problema plačiai naudojama inžinerinėje praktikoje. Liečiamosios plokštumos taip pat naudojamos geometrinių figūrų, apribotų uždarais paviršiais, kontūrams konstruoti. Teoriškai plokštumos, liečiančios paviršių, yra naudojamos diferencialinėje geometrijoje paviršiaus savybėms tirti sąlyčio taško srityje.

Pagrindinės sąvokos ir apibrėžimai

Paviršiaus liestinė turėtų būti laikoma ribine sekanto plokštumos padėtimi (pagal analogiją su kreivės liestine, kuri taip pat apibrėžiama kaip ribinė sekanto padėtis).

Plokštuminė paviršiaus liestinė tam tikrame paviršiaus taške yra visų tiesių – liestinių, nubrėžtų į paviršių per tam tikrą tašką, rinkinys.

Diferencialinėje geometrijoje įrodyta, kad visos įprastame taške nubrėžto paviršiaus liestinės yra lygiagrečios (priklausančios tai pačiai plokštumai).

Išsiaiškinkime, kaip nubrėžti tiesią liniją, liečiančią paviršių. Paviršiaus β liestinė t taške M, nurodytame paviršiuje (203 pav.), reiškia ribinę sekanto l j padėtį, kertančią paviršių dviejuose taškuose (MM 1, MM 2, ..., MM n), kai susikirtimo taškai sutampa (M ≡ M n , l n ≡ l M). Akivaizdu, kad (M 1, M 2, ..., M n) ∈ g, nes g ⊂ β. Iš to, kas išdėstyta pirmiau, pateikiamas toks apibrėžimas: Paviršiaus liestinė yra tiesi linija, kurios liestinė bet kuriai paviršiui priklausančiai kreivei.

Kadangi plokštumą apibrėžia dvi susikertančios tiesės, norint apibrėžti paviršiaus liestinę tam tikrame taške, pakanka per šį tašką nubrėžti dvi savavališkas paviršiui priklausančias linijas (geriausia paprastos formos) ir sudaryti liestinės kiekvienas iš jų šių linijų susikirtimo taške . Sudarytos liestinės vienareikšmiškai nustato liestinės plokštumą. Vaizdinis plokštumos α liestinės su paviršiumi β tam tikrame taške M vaizdas pateiktas Fig. 204. Šis paveikslas taip pat rodo normalųjį n paviršiui β.

Paviršiaus normalioji tam tikrame taške yra tiesi linija, statmena liestinės plokštumai ir einanti per liesties tašką.

Paviršiaus susikirtimo linija su plokštuma, einančia per normaliąją, vadinama normaliąja paviršiaus pjūviu. Priklausomai nuo paviršiaus tipo, liestinės plokštumoje gali būti vienas arba keli taškai (linija) su paviršiumi. Lietimo linija tuo pat metu gali būti ir paviršiaus susikirtimo su plokštuma linija.

Taip pat pasitaiko atvejų, kai paviršiuje yra taškai, kuriuose neįmanoma nubrėžti paviršiaus liestinės; tokie taškai vadinami vienaskaita. Kaip vienaskaitos taškų pavyzdį galime pateikti taškus, priklausančius liemens paviršiaus grįžtamajam kraštui, arba sukimosi paviršiaus dienovidinio susikirtimo tašką su jo ašimi, jei dienovidinis ir ašis nesikerta dešinėje. kampai.

Prisilietimo tipai priklauso nuo paviršiaus kreivumo pobūdžio.

Paviršiaus kreivumas

Paviršiaus kreivumo klausimus nagrinėjo prancūzų matematikas F. Dupinas (1784-1873), pasiūlęs vizualų būdą, kaip pavaizduoti normalių paviršiaus pjūvių kreivumo pokyčius.

Norėdami tai padaryti, plokštumoje, liečiančioje nagrinėjamą paviršių taške M (205, 206 pav.), ant liestinių klojami segmentai, lygūs šių sekcijų atitinkamų kreivio spindulių verčių kvadratinėms šaknims. įprastos sekcijos abiejose šio taško pusėse. Taškų rinkinys – atkarpų galai nusako kreivę, vadinamą Dupino indikatorius. Dupino rodiklio konstravimo algoritmą (205 pav.) galima parašyti:

1. M ∈ α, M ∈ β ∧ α β;

2. = √(R l 1), = √(R l 2),..., = √(R l n)

kur R yra kreivio spindulys.

(A 1 ∪ A 2 ∪ ... ∪ A n) yra Dupino rodiklis.

Jei paviršiaus Dupino indikatorius yra elipsė, tada taškas M vadinamas elipsiniu, o paviršius vadinamas paviršiumi su elipsiniais taškais.(206 pav.). Šiuo atveju liestinės plokštuma turi tik vieną bendrą tašką su paviršiumi, o visos paviršiui priklausančios ir nagrinėjamame taške susikertančios tiesės yra vienoje liestinės plokštumos pusėje. Paviršių su elipsiniais taškais pavyzdžiai yra: apsisukimo paraboloidas, apsisukimo elipsoidas, sfera (šiuo atveju Dupino indikatorius yra apskritimas ir kt.).

Nubrėžiant liemens plokštumą, plokštuma palies šį paviršių išilgai tiesios generatricos. Šios linijos taškai vadinami parabolinis, o paviršius yra paviršius su paraboliniais taškais. Dupino indikatorius šiuo atveju yra dvi lygiagrečios tiesės (207 pav.*).

Fig. 208 parodytas paviršius, susidedantis iš taškų, kuriuose

* Antros eilės kreivė – parabolė – tam tikromis sąlygomis gali suskilti į dvi realias lygiagrečias tieses, dvi įsivaizduojamas lygiagrečias linijas, dvi sutampančius tieses. Fig. 207 turime reikalą su dviem realiomis lygiagrečiomis tiesėmis.

Bet kuri liestinės plokštuma kerta paviršių. Toks paviršius vadinamas hiperbolinis, o jam priklausantys taškai yra hiperboliniai taškai. Dupino indikatorius šiuo atveju yra hiperbolė.

Paviršius, kurio visi taškai yra hiperboliniai, turi balno formą (įstriža plokštuma, vieno lakšto hiperboloidas, įgaubti sukimosi paviršiai ir kt.).

Viename paviršiuje gali būti įvairių tipų taškų, pavyzdžiui, liemens paviršiuje (209 pav.) taškas M yra elipsės formos; taškas N yra parabolinis; taškas K yra hiperbolinis.

Diferencialinės geometrijos metu įrodyta, kad normalios pjūviai, kurių kreivės vertės K j = 1/ R j (kur R j yra nagrinėjamos pjūvio kreivio spindulys), turi kraštutines vertes, yra dviejose viena kitai statmenos plokštumos.

Tokie kreivumai K 1 = 1/R max. K 2 = 1/R min vadinamos pagrindinėmis reikšmėmis, o vertės H = (K 1 + K 2)/2 ir K = K 1 K 2 yra atitinkamai vidutinis paviršiaus kreivumas ir bendras ( Gauso) paviršiaus kreivumą nagrinėjamame taške. Elipsiniams taškams K > 0, hiperboliniams taškams K

Monge diagramos paviršiaus liestinės plokštumos nurodymas

Žemiau, naudodami konkrečius pavyzdžius, parodysime plokštumos, liečiančios paviršių su elipsiniu (1 pavyzdys), paraboliniu (2 pavyzdys) ir hiperboliniu (3 pavyzdys) taškais, konstrukciją.

PAVYZDYS 1. Sukurkite plokštumą α, kurios liestinė β sukimosi paviršiui su elipsiniais taškais. Panagrinėkime du šios problemos sprendimo variantus: a) tašką M ∈ β ir b) tašką M ∉ β

Variantas a (210 pav.).

Liestinės plokštumą lemia dvi liestinės t 1 ir t 2, nubrėžtos taške M į paviršiaus β lygiagretę ir dienovidinį.

Paviršiaus β lygiagrečios h liestinės t 1 projekcijos bus t" 1 ⊥ (S"M") ir t" 1 || x ašis Paviršiaus β dienovidinio d, einančio per tašką M, liestinės t" 2 horizontali projekcija sutaps su dienovidinio horizontalia projekcija. Norint rasti liestinės t" 2 frontalią projekciją, dienovidinio plokštuma γ(γ ∋ M) perkeliama į padėtį γ sukantis aplink paviršiaus ašį β 1, lygiagrečią plokštumai π 2. Šiuo atveju taškas M → M 1 (M" 1, M" 1) liestinės t" 2 rarr; t" 2 1 projekcija nustatoma pagal (M" 1 S"). Jei dabar grąžinsime plokštumą γ 1 į pradinę padėtį, tai taškas S" liks savo vietoje (kaip priklausantis sukimosi ašiai), o M" 1 → M" ir liestinės t" 2 frontalioji projekcija išliks. būti nustatytas (M" S")

Dvi liestinės t 1 ir t 2, susikertančios taške M ∈ β, apibrėžia plokštumą α, liečiančią paviršių β.

Variantas b (211 pav.)

Norint sudaryti paviršiaus, einančio per paviršiui nepriklausantį tašką, liestinę, reikia vadovautis šiais svarstymais: per tašką, esantį už paviršiaus, susidedantį iš elipsinių taškų, galima nubrėžti daug plokštumų, liečiančių paviršių. Šių paviršių apvalkalas bus tam tikras kūgio formos paviršius. Todėl, jei nėra papildomų nurodymų, tada problema turi daug sprendimų ir šiuo atveju redukuojama iki kūginio paviršiaus γ liestinės tam tikro paviršiaus β.

Fig. 211 parodyta kūginio paviršiaus γ, liečiančio sferą β, konstrukcija. Bet kuri kūginio paviršiaus γ liestinė α bus paviršiaus β liestinė.

Norėdami sukurti paviršiaus γ projekcijas iš taškų M" ir M" nubrėžiame apskritimų h" ir f" liestinės – sferos projekcijas. Pažymėkite lietimo taškus 1 (1" ir 1"), 2 (2" ir 2"), 3 (3" ir 3") ir 4 (4" ir 4"). Horizontali apskritimo projekcija – kūginio paviršiaus ir rutulio liestinės linija projektuojama į [ 1"2"] Norėdami rasti elipsės taškus, į kuriuos šis apskritimas bus projektuojamas į priekinę projekcijų plokštumą, naudosime sferos paralelės.

Fig. 211 tokiu būdu nustatomos taškų E ir F (E" ir F") priekinės projekcijos. Turėdami kūginį paviršių γ, sukonstruojame jam liestinę α. Grafikos pobūdis ir seka

Konstrukcijos, kurias tam reikia atlikti, pateiktos sekančiame pavyzdyje.

2 PAVYZDYS Sukurkite paviršiaus α liestinę α su paraboliniais taškais

Kaip ir 1 pavyzdyje, nagrinėjame du sprendinius: a) taškas N ∈ β; b) taškas N ∉ β

Variantas a (212 pav.).

Kūginis paviršius reiškia paviršius su paraboliniais taškais (žr. 207 pav.) Plokštuma, liečianti kūginį paviršių, liečia jį tiesia linija.

1) per nurodytą tašką N nubrėžkite generatorių SN (S"N" ir S"N");

2) kreiptuvu d pažymėkite generatoriaus (SN) susikirtimo tašką: (SN) ∩ d = A;

3) taip pat pūs į liestinę t į d taške A.

Generatorius (SA) ir jį kertanti liestinė t apibrėžia kūginio paviršiaus β liestinę α duotame taške N*.

Nubrėžti plokštumą α, liečiančią kūginį paviršių β ir einančią per tašką N, nepriklauso

* Kadangi paviršius β susideda iš parabolinių taškų (išskyrus viršūnę S), tai liestinės plokštumai α jam bus bendras ne vienas taškas N, o tiesė (SN).

spaudžiant tam tikrą paviršių, būtina:

1) per duotą tašką N ir kūginio paviršiaus β viršūnę S nubrėžkite tiesę a (a" ir a") ;

2) nustatyti šios tiesės H a horizontalųjį pėdsaką;

3) per H a nubrėžiamos kreivės h 0β liestinės t" 1 ir t" 2 - horizontalus kūginio paviršiaus pėdsakas;

4) sujunkite liestinės taškus A (A" ir A") ir B (B" ir B") su kūginio paviršiaus viršūne S (S" ir S").

Susikertančios tiesės t 1, (AS) ir t 2, (BS) nustato norimas liestinės plokštumas α 1 ir α 2

3 PAVYZDYS. Sukurkite paviršiaus β liestinę α su hiperboliniais taškais.

Taškas K (214 pav.) yra globoido paviršiuje (vidiniame žiedo paviršiuje).

Norint nustatyti liestinės plokštumos α padėtį, būtina:

1) per tašką K nubrėžkite lygiagretę su paviršiumi β h(h", h");

2) per tašką K" nubrėžkite liestinę t" 1 (t" 1 ≡ h");

3) norint nustatyti dienovidinio pjūvio liestinės projekcijų kryptis, per tašką K ir paviršiaus ašį reikia nubrėžti plokštumą γ, horizontali projekcija t" 2 sutaps su h 0γ; statyti liestinės t" 2 frontalią projekciją, pirmiausia perkeliame plokštumą γ, sukdami ją aplink sukimosi paviršiaus ašį į padėtį γ 1 || π 2. Šiuo atveju dienovidinio pjūvis plokštuma γ susilygins su kairiuoju priekinės projekcijos kontūro lanku - puslankiu g".

Taškas K (K, K"), priklausantis dienovidinio pjūvio kreivei, pasislinks į padėtį K 1 (K" 1, K" 1). Per K" 1 nubrėžiame frontalinę liestinės t" 2 1 projekciją, sujungtą su plokštuma γ 1 || π 2 padėtį ir pažymėkite jos susikirtimo tašką su priekine sukimosi ašies projekcija S" 1. Grąžiname plokštumą γ 1 į pradinę padėtį, taškas K" 1 → K" (taškas S" 1 ≡ S") Liestinės t" 2 frontalioji projekcija nustatoma taškais K" ir S".

Liestinės t 1 ir t 2 apibrėžia norimą liestinės plokštumą α, kuri kerta paviršių β išilgai kreivės l.

PAVYZDYS 4. Taške K pastatykite paviršiaus β liestinę α. Taškas K yra vieno lapo sukimosi hiperboloido paviršiuje (215 pav.).

Šią problemą galima išspręsti laikantis ankstesniame pavyzdyje naudoto algoritmo, tačiau atsižvelgiant į tai, kad vieno lapo sukimosi hiperboloido paviršius yra valdomas paviršius, turintis dvi tiesių generatorių šeimas, o kiekvienas generatorius po vieną. šeima susikerta su visais kitos šeimos generatoriais (žr. § 32, 138 pav.). Per kiekvieną šio paviršiaus tašką galima nubrėžti dvi susikertančias tiesias linijas – generatorius, kurios vienu metu bus liestinės su vieno lapo sukimosi hiperboloido paviršiumi.

Šios liestinės apibrėžia liestinės plokštumą, tai yra, plokštuma, liečianti vieno lapo sukimosi hiperboloido paviršių, kerta šį paviršių išilgai dviejų tiesių g 1 ir g 2. Norint sudaryti šių tiesių projekcijas, pakanka perkelti taško K horizontaliąją projekciją ir liestines t" 1 ir t" 2 į horizontalę.

apskritimo projekcija d" 2 - vienalapio sukimosi hiperboloido paviršiaus gerklė; nustatykite taškus 1" ir 2, kuriuose t" 1 ir t" 2 kerta vieną ir nukreipiamuosius paviršius d 1. Iš 1" ir 2" randame 1" ir 2", kurie kartu su K nustato reikalingų linijų frontalines projekcijas.

Paviršius apibrėžiamas kaip taškų, kurių koordinatės atitinka tam tikro tipo lygtį, rinkinys:

F (x , y , z) = 0 (1) (\displaystyle F(x,\,y,\,z)=0\qquad (1))

Jei funkcija F (x , y , z) (\displaystyle F(x,\,y,\,z)) yra ištisinis tam tikru tašku ir jame turi ištisinių dalinių išvestinių, iš kurių bent viena neišnyksta, tada šio taško kaimynystėje bus lygties (1) nurodytas paviršius teisingas paviršius.

Be pirmiau minėtų numanomas patikslinimo būdas, paviršius gali būti apibrėžtas aišku, jei vienas iš kintamųjų, pavyzdžiui, z, gali būti išreikštas kitais:

z = f (x, y) (1 ′) (\displaystyle z=f(x,y)\qquad (1"))

Griežčiau paprastas paviršius yra vienetinio kvadrato interjero homeomorfinio atvaizdavimo (tai yra vienas su vienu ir abipusiai nenutrūkstamo kartografavimo) vaizdas. Šiam apibrėžimui galima suteikti analitinę išraišką.

Plokštumoje su stačiakampe koordinačių sistema u ir v duotas kvadratas, kurios vidinių taškų koordinatės tenkina nelygybes 0< u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").

Pavyzdys paprastas paviršius yra pusrutulis. Visa sfera nėra paprastas paviršius. Dėl to reikia toliau apibendrinti paviršiaus sąvoką.

Erdvės poaibis, kurio kiekvienas taškas turi kaimynystę, kuri yra paprastas paviršius, paskambino teisingas paviršius .

Paviršius diferencialinėje geometrijoje

Helicoid

Katenoidas

Metrika vienareikšmiškai nenustato paviršiaus formos. Pavyzdžiui, sraigto ir katenoido metrika, atitinkamai parametrizuota, sutampa, tai yra, tarp jų sričių yra atitikimas, kuris išsaugo visus ilgius (izometrija). Savybės, kurios išsaugomos atliekant izometrines transformacijas, vadinamos vidinė geometrija paviršiai. Vidinė geometrija nepriklauso nuo paviršiaus padėties erdvėje ir nekinta jį lenkiant be įtempimo ar suspaudimo (pavyzdžiui, kai cilindras sulenktas į kūgį).

Metriniai koeficientai E , F , G (\displaystyle E,\ F,\ G) nustatyti ne tik visų kreivių ilgius, bet ir apskritai visų paviršiaus viduje atliktų matavimų (kampų, plotų, kreivumo ir kt.) rezultatus. Todėl viskas, kas priklauso tik nuo metrikos, reiškia vidinę geometriją.

Normalus ir normalus skyrius

Normalieji vektoriai paviršiaus taškuose

Viena iš pagrindinių paviršiaus savybių yra jo normalus- vieneto vektorius, statmenas liestinės plokštumai tam tikrame taške:

m = [ r u ′ , r v ′ ] |.

[ r u ′ , r v ′ ] |

(\displaystyle \mathbf (m) =(\frac ([\mathbf (r"_(u)) ,\mathbf (r"_(v)) ])(|[\mathbf (r"_(u)) ,\mathbf (r"_(v)) ]|))) Normalo ženklas priklauso nuo koordinačių pasirinkimo. Paviršiaus atkarpa plokštuma, kurioje yra paviršiaus normalioji tam tikrame taške, sudaro tam tikrą kreivę, vadinamą

normalus skyrius paviršiai. Pagrindinis normalios atkarpos normalus sutampa su normaliu paviršiui (iki ženklo). Jei kreivė ant paviršiaus nėra normali pjūvis, tada jos pagrindinė normalioji sudaro tam tikrą kampą su paviršiaus normalia θ (\displaystyle \theta ). Tada kreivumas k (\displaystyle k) normalioji atkarpa (su ta pačia liestine) pagal Meunier formulę:

k n = ± k cos θ (\displaystyle k_(n)=\pm k\,\cos \,\theta )

Įvairių paviršiaus apibrėžimo metodų normaliojo vieneto vektoriaus koordinatės pateiktos lentelėje:

	Normalios koordinatės paviršiaus taške
numanomas paskyrimas	(∂ F ∂ x ; ∂ F ∂ y ; ∂ F ∂ z) (∂ F ∂ x) 2 + (∂ F ∂ y) 2 + (∂ F ∂ z) 2 (\displaystyle (\frac (\left(()) \frac (\partial F)(\partial x));\,(\frac (\partial F)(\partial y));\,(\frac (\partial F)(\partial z))\right) )(\sqrt (\left((\frac (\partial F)(\partial x))\right)^(2)+\left((\frac (\partial F)(\partial y))\right) ^(2)+\left((\frac (\partial F)(\partial z))\right)^(2)))))
aiškus pavedimas	(− ∂ f ∂ x ; − ∂ f ∂ y ; 1) (∂ f ∂ x) 2 + (∂ f ∂ y) 2 + 1 (\displaystyle (\frac (\left(-(\frac (\partial f)) )(\partial x));\,-(\frac (\partial f)(\partial y));\,1\right))(\sqrt (\left((\frac (\partial f)(\)) dalinė x))\dešinė)^(2)+\left((\frac (\partial f)(\partial y))\right)^(2)+1))))
parametrinė specifikacija	(D (y, z) D (u, v) ; D (z, x) D (u, v) ; D (x, y) D (u, v)) (D (y, z) D (u) , v)) 2 + (D (z , x) D (u , v)) 2 + (D (x, y) D (u , v)) 2 (\displaystyle (\frac (\left((\frac)) (D(y,z))(D(u,v)));\,(\frac (D(z,x))(D(u,v)));\,(\frac (D(x) ,y))(D(u,v)))\right))(\sqrt (\left((\frac (D(y,z))(D(u,v)))\right)^(2 )+\left((\frac (D(z,x))(D(u,v)))\right)^(2)+\left((\frac (D(x,y))(D( u,v)))\dešinė)^(2))))

Čia D (y , z) D (u , v) = |.

y u ′ y v ′ z u ′ z v ′ | , D (z , x) D (u , v) = |.

z u ′ z v ′ x u ′ x v ′ |

, D (x, y) D (u, v) = | x u ′ x v ′ y u ′ y v ′ |(\displaystyle (\frac (D(y,z))(D(u,v)))=(\begin(vmatrix)y"_(u)&y"_(v)\\z"_(u) &z"_(v)\end(vmatrix)),\quad (\frac (D(z,x))(D(u,v)))=(\begin(vmatrix)z"_(u)&z" _(v)\\x"_(u)&x"_(v)\end(vmatrix)),\quad (\frac (D(x,y))(D(u,v)))=(\ pradžia(vmatrica)x"_(u)&x"_(v)\\y"_(u)&y"_(v)\end(vmatrix)))

Visos išvestinės imamos taške (x 0, y 0, z 0) (\displaystyle (x_(0),y_(0),z_(0))) Ir e 2 (\displaystyle e_(2)), kurioje normalus kreivumas įgauna minimalias ir didžiausias vertes; šios kryptys vadinamos pagrindinis. Išimtis yra atvejis, kai normalus kreivumas visomis kryptimis yra vienodas (pavyzdžiui, šalia sferos arba apsisukimo elipsoido pabaigoje), tada visos kryptys taške yra pagrindinės.

Paviršiai su neigiamu (kairėje), nuliniu (centru) ir teigiamu (dešinėje) kreivumu.

Įprasti kreiviai pagrindinėmis kryptimis vadinami pagrindiniai išlinkimai; paskirkime juos κ 1 (\displaystyle \kappa _(1)) Ir κ 2 (\displaystyle \kappa _(2)). Dydis:

K = κ 1 κ 2 (\displaystyle K=\kappa _(1)\kappa _(2))

Apibrėžimas. Taškas, esantis ant antros eilės paviršiaus, apibrėžto ODSC atžvilgiu pagal bendrąją lygtį (1), vadinamas nevienaskaitiu, jei tarp trijų skaičių: yra bent vienas, kuris nėra lygus nuliui.

Taigi taškas, esantis ant antros eilės paviršiaus, nėra ypatingas tada ir tik tada, kai yra jo centras, kitaip, kai paviršius yra kūginis, o taškas yra šio paviršiaus viršūnė.

Apibrėžimas. Antros eilės paviršiaus liestinė tam tikrame neypatingame jo taške yra tiesė, kuri eina per šį tašką, kerta antros eilės paviršių dvigubame taške arba yra tiesinis paviršiaus generatorius.

3 teorema. Antrosios eilės paviršiaus liestinės linijos tam tikrame neypatingame jo taške yra vienoje plokštumoje, vadinamoje nagrinėjamo taško paviršiaus liestinės plokštuma. Liečiamosios plokštumos lygtis turi

Įrodymas. Tegul , , yra parametrinės lygtys tiesės, einančios per nevienetinį antros eilės paviršiaus tašką, pateiktą pagal (1) lygtį. Į (1) lygtį pakeitę , , vietoj , , gauname:

Kadangi taškas yra paviršiuje (1), mes taip pat randame iš (3) lygties (ši reikšmė atitinka tašką ). Kad tiesės susikirtimo taškas su paviršiumi (1) būtų dvigubas arba kad linija būtų visiškai ant paviršiaus, būtina ir pakanka, kad būtų įvykdyta lygybė:

Jei šiuo atveju:

Tada tiesės ir paviršiaus (1) susikirtimo taškas yra dvigubas. Ir jei:

Tada tiesi linija yra visiškai ant paviršiaus (1).

Iš ryšių (4) ir , išplaukia, kad bet kurio taško, esančio bet kurioje paviršiaus (1) liestinėje, koordinatės , , tenkina lygtį:

Ir atvirkščiai, jei kito taško koordinatės tenkina šią lygtį, tada vektoriaus koordinatės tenkina ryšį (4), o tai reiškia, kad tiesė yra nagrinėjamo paviršiaus liestinė.

Kadangi taškas yra ne vienaskaitos taškas paviršiaus (1), tada tarp skaičių , yra bent vienas, kuris nėra lygus nuliui; Tai reiškia, kad (5) lygtis yra pirmojo laipsnio lygtis . Tai plokštumos, liečiančios paviršių (1) tam tikrame neypatingame jo taške, lygtis.

Remiantis kanoninėmis antros eilės paviršių lygtimis, nesunku sudaryti elipsoido, hiperboloido ir kt. liestinių plokštumų lygtis. tam tikrame jų taške.

1). Elipsoido liestinės plokštuma:

2). Vieno lapo ir dviejų lakštų hiperboloidų liestinės plokštuma:

3). Elipsinių ir hiperbolinių paraboloidų liestinės plokštuma:

§ 161. Liečiamosios plokštumos susikirtimas su antros eilės paviršiumi.

Paimkime nevienetinį antros eilės paviršiaus tašką kaip ODSC ašies koordinačių pradžią ir pastatykime jį į paviršiaus liestinę taške . Tada bendrojoje paviršiaus (1) lygtyje laisvasis narys yra lygus nuliui: , o plokštumos, liečiančios paviršių pradinėje vietoje, forma turėtų būti: .

Bet plokštumos, einančios per pradžią, lygtis turi tokią formą: .

Ir kadangi ši lygtis turi būti lygiavertė lygčiai, tada , , .

Taigi pasirinktoje koordinačių sistemoje paviršiaus lygtis (1) turėtų būti tokia:

Ir atvirkščiai, jei , tai lygtis (6) yra paviršiaus, einančio per koordinačių pradžią, lygtis, o plokštuma yra šio paviršiaus liestinė taške. Tiesės, iš kurios paviršiaus liestinės plokštuma taške kerta paviršių (6), lygtis yra tokia:

Jei . Tai yra invariantas antros eilės eilučių invariantų teorijoje. (7) lygtis

Tai yra antrosios eilės tvarka. Pagal šios eilutės formą yra invariantas, todėl:

Nes čia yra dvi įsivaizduojamos susikertančios linijos.

Ties - dvi tikros susikertančios linijos.

Jei , bet bent vienas iš koeficientų , , nėra lygus nuliui, tai susikirtimo linija (7) yra dvi sutampančios tiesės.

Galiausiai, jei , tai lėktuvas

yra tam tikro paviršiaus dalis, todėl pats paviršius skyla į plokštumų porą

§ 162. Elipsiniai, hiperboliniai arba paraboliniai antros eilės paviršiaus taškai.

1. Tegul antros eilės paviršiaus liestinės plokštuma taške kerta jį išilgai dviejų įsivaizduojamų susikertančių tiesių. Šiuo atveju taškas vadinamas elipsiniu paviršiaus tašku.

2. Tegul antros eilės paviršiaus liestinės plokštuma taške kerta ją išilgai dviejų realių tiesių, susikertančių sąlyčio taške. Šiuo atveju taškas vadinamas hiperboliniu paviršiaus tašku.

3. Tegul antros eilės paviršiaus liestinės plokštuma taške kerta ją išilgai dviejų sutampančių tiesių. Šiuo atveju taškas vadinamas paraboliniu paviršiaus tašku.

4 teorema. Tegul antros eilės paviršius ODSC atžvilgiu yra pateiktas (1) lygtimi, o ši (1) lygtis yra tikrojo antros eilės neirstančio paviršiaus lygtis. Tada jei ; tada visi paviršiaus taškai yra elipsės formos.

Įrodymas. Įveskime naują koordinačių sistemą, koordinačių pradžią pasirinkdami bet kurį duoto paviršiaus nevienetinį tašką ir taške išdėstydami ašis ir plokštumos liestinę. Lygtis (1) naujoje koordinačių sistemoje transformuojama į formą:

Kur. Apskaičiuokime šios lygties invariantą.

Kadangi ženklas nesikeičia pereinant iš vieno ODSC į kitą ODSC, ženklai yra priešingi, todėl, jei , tada ; ir, kaip matyti iš klasifikacijos (žr. § 161), paviršiaus liestinė plokštuma taške kerta paviršių išilgai dviejų įsivaizduojamų susikertančių tiesių, t.y. - elipsinis taškas.

2) Vieno lapo hiperboloidas ir hiperbolinis paraboloidas susideda iš hiperbolinių taškų.

3) Tikras antros eilės kūgis (išskyrus viršūnę), elipsinis (tikrasis), hiperbolinis ir parabolinis cilindras susideda iš parabolinių taškų.

Parabolinis cilindras.

Norint nustatyti parabolinio cilindro vietą, pakanka žinoti:

1) simetrijos plokštuma, lygiagreti cilindro generatrams;

2) cilindro liestinės plokštuma, statmena šiai simetrijos plokštumai;

3) vektorius, statmenas šiai liestinės plokštumai ir nukreiptas į cilindro įdubimą.

Jei bendroji lygtis apibrėžia parabolinį cilindrą, ją galima perrašyti taip:

Rinksim m kad lėktuvai

būtų statmenos viena kitai:

Šia verte m lėktuvas

bus simetrijos plokštuma, lygiagreti cilindro generatrams.

Lėktuvas

bus cilindro liestinė, statmena nurodytai simetrijos plokštumai, ir vektorius

bus statmena rastai liestinės plokštumai ir nukreipta į cilindro įdubimą.