ვინც სკოლაში ყურადღებით უსმენდა გეომეტრიის მასწავლებელს, კარგად იცნობს რა არის ეგვიპტური სამკუთხედი. იგი განსხვავდება სხვა ტიპის მსგავსიდან 90 გრადუსიანი კუთხით მისი სპეციალური ასპექტის თანაფარდობით. როდესაც ადამიანს პირველად ესმის ფრაზა "ეგვიპტური სამკუთხედი", გონზე მოდის დიდებული პირამიდების და ფარაონების სურათები. მაგრამ რას ამბობს ისტორია?
ეგვიპტური გეომეტრიის ექსპერტებს "არპედონაპტი" ეძახდნენ, მათ, ვინც თოკებს აკრავენ. სწორედ თოკების დაჭიმვით დახატეს ორი უმარტივესი და ყველაზე მნიშვნელოვანი ხაზი გეომეტრიაში: სწორი ხაზი და წრე. პირველი, ორ წერტილს შორის თოკის უბრალოდ დაჭიმვით, ოპერაციის ტიპი, რომლის გამოსახულება ჯერ კიდევ არსებობს გამონათქვამებში „ხაზის დახატვა“, „პერპენდიკულარულის დახატვა“; მეორე არის ორი წერტილიდან ერთი მეორის გარშემო ბრუნვის გამომწვევი მიზეზი, რომელიც ფიქსირებულია. შეუძლიათ მათ წარმოიდგინონ ამ ორი ელემენტარული პრაქტიკის განვითარების ხარისხი?
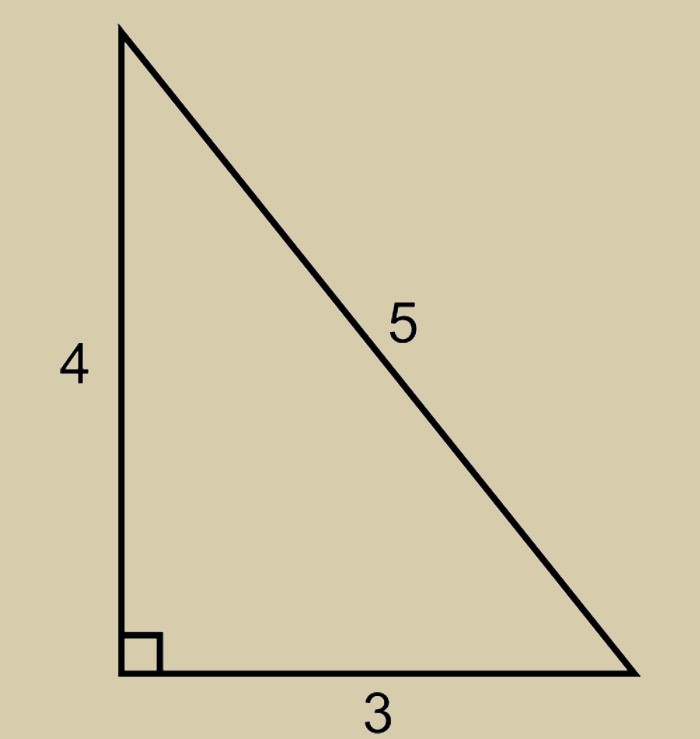
როგორც ყოველთვის, არსებობს რამდენიმე თეორია სახელთან დაკავშირებით "ეგვიპტური სამკუთხედი". ერთ-ერთი მათგანის მიხედვით, ცნობილი პითაგორას თეორემა სწორედ ამ ფიგურის წყალობით გაჩნდა. 535 წელს ძვ. პითაგორა, თალესის რეკომენდაციით, გაემგზავრა ეგვიპტეში, რათა შეევსებინა გარკვეული ხარვეზები მათემატიკისა და ასტრონომიის ცოდნაში. იქ მან ყურადღება გაამახვილა ეგვიპტელი მიწის ამზომველების მუშაობის თავისებურებებზე. ისინი ძალიან უჩვეულო გზითშეასრულეს მართი კუთხით კონსტრუქცია, რომლის გვერდები ერთმანეთთან იყო დაკავშირებული 3-4-5 თანაფარდობით. ამ მათემატიკური სერიამ შედარებით მარტივი გახადა სამივე მხარის კვადრატების ერთი წესით დაკავშირება. ასე გაჩნდა ცნობილი თეორემა. და ეგვიპტური სამკუთხედი არის ზუსტად იგივე ფიგურა, რამაც აიძულა პითაგორა ყველაზე გენიალური გამოსავალი. სხვა ისტორიული მონაცემებით, ფიგურას სახელი დაარქვეს ბერძნებმა: იმ დროს ისინი ხშირად სტუმრობდნენ ეგვიპტეს, სადაც შეეძლოთ დაინტერესდნენ მიწის ამზომველების მუშაობით. არსებობს შესაძლებლობა, რომ, როგორც ხშირად ხდება სამეცნიერო აღმოჩენები, ორივე ამბავი ერთდროულად მოხდა, ამიტომ დარწმუნებით შეუძლებელია იმის თქმა, თუ ვინ იყო პირველი, ვინც მოიფიქრა სახელი "ეგვიპტური სამკუთხედი". მისი თვისებები გასაოცარია და, რა თქმა უნდა, არ შემოიფარგლება მხოლოდ ასპექტის თანაფარდობით. მისი ფართობი და გვერდები წარმოდგენილია მთელი რიცხვებით. ამის წყალობით, მასზე პითაგორას თეორემის გამოყენება საშუალებას გვაძლევს მივიღოთ ჰიპოტენუზისა და ფეხების კვადრატების მთელი რიცხვები: 9-16-25. რა თქმა უნდა, ეს შეიძლება იყოს მხოლოდ დამთხვევა. მაგრამ როგორ შეიძლება ამ შემთხვევაში ავხსნათ ის ფაქტი, რომ ეგვიპტელები „თავიანთ“ სამკუთხედს წმინდად თვლიდნენ? მათ სჯეროდათ მისი ურთიერთკავშირი მთელ სამყაროსთან.
სინამდვილეში, უძველესი ამზომველების პრაქტიკულმა საჭიროებებმა შეიძლება მალე მოითხოვოს ისეთი სამუშაოები, რომლებსაც ჩვენ დღეს ვუწოდებთ „კვადრატსა და კომპასს“ და რასაც ყველაზე სწორად „წრეები და სწორები“ უნდა ვუწოდოთ. ამჟამად ბუნებრივია ქაღალდი გეომეტრიის ბუნებრივ ასპარეზად მივიჩნიოთ, ასე რომ, ჩვენ გვესმის კვადრატებისა და კომპასების გამოყენება, როგორც თვითნებური ლიმიტი, რომელიც დაწესებულია სპეკულაციური სულების მიერ, რომლებიც უპირატესობას ანიჭებდნენ რამდენიმე აქსიომას, ვიდრე მრავალი მოხერხებულობა. ინსტრუმენტები.
აქედან გამომდინარეობს განსხვავება თეორიულ გეომეტრიის ექსპერტს შორის. ამრიგად, ჩვენ მიდრეკილნი ვართ მთლიანად უგულებელვყოთ გეომეტრია „ველში“ ამ „ქაღალდზე“ სასარგებლოდ, რაც არ გვაძლევს საშუალებას გავიგოთ, რომ გეომეტრიული მოქმედებების ველიდან ქაღალდზე გადატანისას, მათ ზოგჯერ სრულიად დასჭირდებათ. სხვადასხვა მეთოდებიდა მეთოდები.
მას შემდეგ, რაც ინფორმაცია ამ უჩვეულო გეომეტრიული ფიგურის შესახებ საჯარო გახდა, მსოფლიომ დაიწყო სხვა მსგავსი სამკუთხედების ძებნა მთელი რიცხვებით. აშკარა იყო, რომ ისინი არსებობდნენ. მაგრამ კითხვის მნიშვნელობა არ იყო უბრალოდ მათემატიკური გამოთვლების შესრულება, არამედ "წმინდა" თვისებების შემოწმება. ეგვიპტელები, მთელი მათი უჩვეულოობის მიუხედავად, არასოდეს ითვლებოდნენ სულელად - მეცნიერებს ჯერ კიდევ არ შეუძლიათ ახსნან ზუსტად როგორ აშენდა პირამიდები. და აქ, უცებ, ჩვეულებრივ ფიგურას მიაწერეს კავშირი ბუნებასთან და სამყაროსთან. და, მართლაც, ნაპოვნი ლურსმული ასო შეიცავს მითითებებს სამკუთხედის მსგავსადგვერდით, რომლის ზომა აღწერილია 15-ნიშნა რიცხვით. ამჟამად ეგვიპტური სამკუთხედი, რომლის კუთხეებია 90 (მარჯვნივ), 53 და 37 გრადუსი, გვხვდება სრულიად მოულოდნელ ადგილებში. მაგალითად, ჩვეულებრივი წყლის მოლეკულების ქცევის შესწავლისას აღმოჩნდა, რომ ცვლილებას თან ახლავს მოლეკულების სივრცითი კონფიგურაციის რესტრუქტურიზაცია, რომელშიც ხედავთ... იგივე ეგვიპტურ სამკუთხედს. თუ გავიხსენებთ, რომ ის სამი ატომისგან შედგება, მაშინ შეგვიძლია ვისაუბროთ პირობით სამ მხარეს. რა თქმა უნდა, ჩვენ არ ვსაუბრობთ ცნობილი თანაფარდობის სრულ დამთხვევაზე, მაგრამ მიღებული რიცხვები ძალიან, ძალიან ახლოს არის საჭიროებთან. ამიტომაც აღიარეს ეგვიპტელებმა თავიანთი სამკუთხედი „3-4-5“ სიმბოლურ გასაღებად ბუნებრივი ფენომენიდა სამყაროს საიდუმლოებები? წყალი ხომ, მოგეხსენებათ, სიცოცხლის საფუძველია. ეჭვგარეშეა, ცნობილი ეგვიპტელი მოღვაწის შესწავლის დასასრული ნაადრევია. მეცნიერება არასოდეს ჩქარობს დასკვნებს, ცდილობს დაამტკიცოს თავისი ვარაუდები. და ჩვენ შეგვიძლია მხოლოდ დაველოდოთ და გაოცებული ვიყოთ ცოდნით
არ უნდა დაგვავიწყდეს, რომ გეგმის სიზუსტე ბევრად უფრო მნიშვნელოვანია, ვიდრე ქაღალდზე. არქიტექტორს, რომელსაც აქვს მკაფიო წარმოდგენა მთლიანი გეგმის შესახებ და რომელსაც ახსოვს პროცესი, რომელიც მან მიჰყვა მის გასავლელად, დასჭირდება დიზაინი. შედარებით უახლესი რუქები, ისევე როგორც ძველი რუკები, რომლებიც აუცილებლად შედგენილი იყო ელემენტარული ხელსაწყოებითა და საყრდენებით, ზუსტად არ ასახავს მიწის ნაკვეთის საზღვრებს. სინამდვილეში ეს შეუძლებელია, რადგან პროცენტული შეცდომაც კი - ყველაზე მცირე, რაც შეიძლება მოხდეს საკმარისად დიდი მასშტაბით - წარმოქმნის აბსოლუტურ შეცდომას, რომელიც ნაკლებად სავარაუდოა, რომ მიღებულ იქნას ველზე.
ეგვიპტური სამკუთხედი და მისი თვისებები ცნობილი იყო უძველესი დროიდან. ეს ფიგურა ფართოდ გამოიყენებოდა მშენებლობაში სწორი კუთხეების მონიშვნისა და ასაგებად.
ეგვიპტური სამკუთხედის ისტორია
ამ გეომეტრიული დიზაინის შემქმნელია ანტიკურობის ერთ-ერთი უდიდესი მათემატიკოსი პითაგორა. სწორედ მისი მათემატიკური კვლევის წყალობით შეგვიძლია სრულად გამოვიყენოთ ამ გეომეტრიული სტრუქტურის ყველა თვისება მშენებლობაში.
ამ შემთხვევაში ფუნდამენტურია აღსაწერი ობიექტის ფორმისა და ზომის ცოდნა; გეომეტრიის სპეციალისტს არ დაევალება ველზე გამრავლება იმ სიზუსტით, რომელიც არ არის ხელმისაწვდომი ქაღალდზე. იგივე ემართება მათემატიკოსს, რომლის წაკითხვის სიზუსტე საერთოდ არ გამოდგება დემონსტრაციებში. ქაღალდზე გეომეტრია ცვლის ველზე მოქმედებების სიზუსტეს გონებრივი პროცესის გეომეტრიით.
პირიქით, ლოგიკიდან მატერიალურ სიზუსტემდე, მასშტაბის აუცილებელი გაფართოების შედეგად გეგმიდან მის რეალურ შექმნაზე გადასასვლელად, თოკის დაჭიმვის აქტი დარჩა ერთ-ერთ ძირითად ოპერაციად, ვინაიდან ძველ ეგვიპტემდე და Უძველესი საბერძნეთი. ეს პრაქტიკა დღემდე უცვლელი დარჩა, მხოლოდ გარკვეული ოპტიკური ინსტრუმენტების გამოგონებითა და გაუმჯობესებით გადაცემული. მიუხედავად იმისა, რომ საკმაოდ მარტივია პერპენდიკულარის დახატვა ქაღალდზე სახაზავებისა და კვადრატების გამოყენებით, იგივე ქმედება ველზე იგივე სიზუსტით მოითხოვს რადიკალურად განსხვავებულ მეთოდებს.
შეიძლება ვივარაუდოთ, რომ მათემატიკური უნარები პითაგორას საშუალებას აძლევდა შეემჩნია ნიმუში სტრუქტურის ფორმებში. Შემდგომი განვითარებამოვლენები ადვილად წარმოსადგენია. საბაზისო ანალიზმა და დასკვნების გამოტანამ შექმნა ისტორიაში ერთ-ერთი ყველაზე მნიშვნელოვანი ფიგურა. სავარაუდოდ, სწორედ კეოპსის პირამიდა აირჩიეს პროტოტიპად მისი თითქმის სრულყოფილი პროპორციების გამო.
მინდორში კვადრატი გამოუსადეგარია, რადგან ძალიან მცირეა ფორმების ზომასთან მიმართებაში. მაშინაც კი, თუ კვადრატი უკიდურესად ზუსტია, პერპენდიკულარი, რომელსაც შეუძლია დახატოს, მიაღწევს თავის უდიდეს ან უმცირეს მეტრს. თუ ჩვენ გვჭირდება კვადრატის მონიშვნა თითო მხარეს 30 მეტრით, ეს ხაზი უნდა გავაგრძელოთ 30-ჯერ. ეს ისეთი არაზუსტი ოპერაცია იქნებოდა, რომ ალბათ ისეთივე შედეგს გამოიღებდა, თითქოს სწორი კუთხე უხეშად გაგვეზომა.
ეს ასახვები გვაბრუნებს თავდაპირველ კითხვას: რა მეთოდებს იყენებდნენ ეგვიპტელი მზომები მიწის კვადრატული ნაწილის დასახატად? როგორ მიიღეს კვადრატული კუთხე? მაშასადამე, თუ 12 ერთეულის სიგრძის რგოლ თოკს, რომელიც მონიშნულია სამ წერტილში 3, 4 და 5 დისტანციებზე, სამკუთხედის სახით, რომელსაც წვერო აქვს მონიშნულ წერტილებში, კუთხე სამკუთხედის უმოკლეს გვერდებს შორის არის სწორი კუთხე.
ეგვიპტური სამკუთხედი მშენებლობაში
ამ უნიკალური გეომეტრიული სტრუქტურის თვისებები არის ის, რომ მისი მშენებლობა ყოველგვარი ხელსაწყოების გამოყენების გარეშე საშუალებას გაძლევთ ააგოთ სახლი სწორი კუთხით ყველა ურთიერთობაში.
Მნიშვნელოვანი! რა თქმა უნდა, იდეალურად საუკეთესო ვარიანტი იქნება პროტრატორის ან კვადრატის გამოყენება.
უცნობია, ჩაატარეს თუ არა ეს პროცესი თავის დროზე ძველმა ამზომველებმა, რადგან არ დადასტურდა, რომ ძველ ეგვიპტელებს იცოდნენ, რომ სამკუთხედი 3, 4 და 5 გვერდებით იყო მართკუთხა სამკუთხედი. მაშინაც კი, თუ მათ იციან ამ ან სხვა პითაგორას სამკუთხედების შესახებ, ეს აუცილებლად ნიშნავს, რომ მათ იცოდნენ ბუნება ან თუნდაც როგორ შეექმნათ სწორი კუთხე.
საიდან გაჩნდა ეს ცოდნა? თუნდაც ნაწილობრივი დოკუმენტაციისა და მოწმეების არარსებობის გამო, შეგვიძლია შევეცადოთ პრობლემას სხვა კუთხით მივუდგეთ, მათემატიკური და არა ისტორიული. კითხვა, რომელიც უნდა დავსვათ არის ის, თუ რა განასხვავებს მართ კუთხეს სხვებისგან? ან უკეთესი, რა თვისება აქვს 3, 4 და 5 გვერდების მქონე სამკუთხედის კუთხეს?
ასე რომ, ეგვიპტური სამკუთხედის თვისებები საშუალებას გაძლევთ შექმნათ კუთხეები, რომლებიც სწორია ყველა ურთიერთობაში. სტრუქტურის გვერდებს აქვთ შემდეგი თანაფარდობა ერთმანეთთან:
იმის შესამოწმებლად, დახატეთ თუ არა სწორი ფიგურა, გამოიყენეთ პითაგორას თეორემა, რომელიც ცნობილია სკოლიდან.
ყურადღება! ეგვიპტური სამკუთხედის თვისებები ისეთია, რომ ჰიპოტენუზის კვადრატი უდრის ორი ფეხის კვადრატს.
მყისიერი პასუხი: სხვა სამკუთხედებისგან განსხვავებით, პითაგორა და მათგან უმარტივესი, გვერდებით 3, 4 და 5, შეიძლება შეერთდეს ერთ მხარეს და შემდეგ ისევ მეორე მხარეს. ეს იწვევს სიმეტრიულ კონფიგურაციას, რომელიც მთლიანად ავსებს ყველაფერს თავისუფალი სივრცეარანაირი გადახურვა ან ხარვეზები.
არცერთ სხვა კუთხეს, გარდა მართისა, არ აქვს ეს სიმეტრიული მახასიათებელი, რომელიც ხდება მისი განმარტება გეომეტრიის პირველ სრულ წიგნში, რომელიც ოდესმე მოაღწია ჩვენს დრომდე, ევკლიდეს ელემენტებში. როცა სხვაზე ჩამოვარდნილი სწორი ხაზი იქმნება თანაბარი კუთხეები, ისინი მართლები არიან.
უკეთესი გაგებისთვის ავიღოთ ზემოაღნიშნული დამოკიდებულება და შევადგინოთ პატარა მაგალითი. გავამრავლოთ ხუთი ხუთზე. შედეგად ვიღებთ ჰიპოტენუზას ტოლი 25. გამოვთვალოთ ორი ფეხის კვადრატები. ისინი იქნებიან 16 და 9. შესაბამისად მათი ჯამი იქნება ოცდახუთი.
ამიტომაა, რომ ეგვიპტური სამკუთხედის თვისებები ასე ხშირად გამოიყენება მშენებლობაში. საკმარისია აიღოთ სამუშაო ნაწილი და დახაზოთ სწორი ხაზი. მისი სიგრძე ყოველთვის უნდა იყოს 5-ის ჯერადი. შემდეგ თქვენ უნდა მონიშნოთ ერთი კიდე და გაზომოთ ხაზი, რომელიც იყოფა 4-ზე მისგან, ხოლო 3-ზე მეორედან.
კვადრატული კუთხის ბუნება ის არის, რომ ორი სწორი ხაზის გადაკვეთის შედეგად მიღებული კუთხეები ტოლია. ამის დემონსტრირება შესაძლებელია ქაღალდზე, ქაღალდის დაკეცვით ერთ-ერთი შემაერთებელი ხაზის გასწვრივ და შემოწმებით, რომ მეორე ხაზი იკეცება თავის თავზე.
ამ თვისებას აქვს "კლასიკური" გეომეტრიული დიზაინი ორი წრის მონიშვნისა და შემდეგ მათი კვეთების გაერთიანების შესახებ. ფორმის სიმეტრიული ბუნება საკმაოდ აშკარაა და ეს აშკარა მტკიცებულებაა კუთხეების თანასწორობის შესახებ. უფრო მეტიც, პითაგორას სამკუთხედისგან განსხვავებით, რომელსაც შემდგომი კონსტრუქცია სჭირდება, ამ შემთხვევაში ფორმა მაშინვე გვთავაზობს კვადრატული კუთხის განსაზღვრას კუთხეების ტოლობის მეშვეობით და ამავე დროს თავად აყალიბებს თავის თავს.
ყურადღება! თითოეული სეგმენტის სიგრძე იქნება 4 და 3 სმ (მინიმალური მნიშვნელობებით). ამ ხაზების გადაკვეთა ქმნის მართკუთხა კუთხეს, რომელიც ტოლია 90 გრადუსს.
90 გრადუსიანი სწორი კუთხის აგების ალტერნატიული გზები
როგორც ზემოთ აღინიშნა, საუკეთესო ვარიანტიკვადრატის ან პროტრატორის აღება ადვილი იქნება. ეს ხელსაწყოები გაძლევთ საშუალებას ყველაზე დაბალ ფასადდრო და ძალისხმევა სასურველი პროპორციების მისაღწევად. ეგვიპტური სამკუთხედის მთავარი თვისება მისი მრავალფეროვნებაა. ფიგურის აშენება შესაძლებელია პრაქტიკულად არაფრით თქვენს არსენალში.
ეს ჯერ კიდევ მარტივი ვარაუდებია. ეჭვგარეშეა, ეს პროცესი ნამდვილად უფრო მარტივი და ზუსტია, ვიდრე პირველი. შეიძლება ითქვას, რომ ჩვენ შეგვიძლია აღვნიშნოთ მხოლოდ მოცემული სეგმენტის ცენტრში გამავალი პერპენდიკულური, რომელსაც ასევე უწოდებენ სეგმენტის ღერძს. თუმცა, ადვილი მისახვედრია, რომ თუ გვსურს პერპენდიკულარი ერთ კიდეზე, როგორც კვადრატის დახატვის შემთხვევაში, უნდა გავაორმაგოთ სეგმენტი, გავაგრძელოთ ის იქამდე, სადაც გვინდა დავხატოთ პერპენდიკულარი და შემდეგ გავიმეოროთ წინა პროცესი.
უნდა აღინიშნოს, რომ ყველა ეს მეთოდი განსაკუთრებით შესაფერისია ბრტყელი მიწებისთვის, როგორიცაა ეგვიპტის დაბლობი. თვითმფრინავებთან და ძრავებთან დაკავშირებული ზოგიერთი პრობლემის უკეთ გასაგებად, სამკუთხედების შესასწავლად აუცილებელია ტრიგონომეტრიის ზოგიერთი მათემატიკური იდეის გამოყენება. დავიწყოთ რამდენიმე განმარტებით და ტერმინოლოგიით, რომლებსაც გამოვიყენებთ ამ სლაიდზე. დავიწყოთ იმით რეგულარული სამკუთხედი. მართკუთხა სამკუთხედი არის სამკუთხა ფიგურა, რომლის ერთი კუთხე უდრის 90 გრადუსს.
ძლიერია მშენებლობაში სწორი კუთხემარტივი ბეჭდური მასალები დაგეხმარებათ. მიიღეთ ნებისმიერი ჟურნალი ან წიგნი. ფაქტია, რომ მათი ასპექტის თანაფარდობა ყოველთვის ზუსტად 90 გრადუსია. საბეჭდი მანქანა მუშაობს ძალიან ზუსტად. წინააღმდეგ შემთხვევაში, რულონი, რომელიც ჩაედინება მანქანაში, დაიჭრება არაპროპორციული დახრილი კუთხით.
90 გრადუსიან კუთხეს მართკუთხა კუთხეს უწოდებენ, საიდანაც მართკუთხა სამკუთხედი იღებს თავის სახელს. ეს არის მართკუთხა სამკუთხედის სამი გვერდის ყველაზე გრძელი გვერდი. სიტყვა "ჰიპოტენუზა" მომდინარეობს ორი ბერძნული სიტყვიდან, რაც ნიშნავს "გაჭიმვას", რადგან ის ყველაზე გრძელი მხარეა.
პითაგორას თეორემა არის განცხადება, რომელიც აკავშირებს ნებისმიერი მართკუთხა სამკუთხედის გვერდების სიგრძეებს. ნებისმიერი მართკუთხა სამკუთხედისთვის - ჰიპოტენუზის კვადრატი. უდრის დანარჩენი ორი მხარის კვადრატების ჯამს. ეს მათემატიკურად წერია. ეს თეორემა მრავალ კულტურაში მრავალი სახელით იყო ცნობილი წლების განმავლობაში. ითვლება, რომ მან ეგვიპტეში სწავლის დროს ისწავლა თეორემა. ეგვიპტელებმა ალბათ პითაგორამდე ათასი წლით ადრე იცოდნენ ურთიერთობის შესახებ.
როგორ გავაკეთოთ ეგვიპტური სამკუთხედი თოკის გამოყენებით

ამის თვისებები გეომეტრიული ფიგურაძნელი გადაფასება. გასაკვირი არ არის, რომ ძველმა ინჟინრებმა მინიმალური რესურსების გამოყენებით მისი ჩამოყალიბების მრავალი გზა მოიგონეს.
ერთ-ერთი უმარტივესი არის ეგვიპტური სამკუთხედის ფორმირების მეთოდი მისი ყველა თანმდევი თვისებით მარტივი თოკის გამოყენებით. აიღეთ ძაფი და დაჭერით 12 აბსოლუტურად თანაბარ ნაწილად. მათგან გააკეთეთ ფიგურა 3, 4 და 5 პროპორციებით.
პითაგორამ შედეგი განაზოგადა ნებისმიერ მართკუთხა სამკუთხედზე. თეორემის მრავალი განსხვავებული ალგებრული და გეომეტრიული მტკიცებულება არსებობს. მათი უმეტესობა იწყება კვადრატების აგებით ძირითადი მართკუთხა სამკუთხედის ესკიზზე. ამ გვერდის ზედა სურათზე ჩვენ ვაჩვენებთ სამკუთხედის სამ მხარეს დახატულ კვადრატებს. კვადრატი არის მართკუთხედის განსაკუთრებული შემთხვევა, რომელშიც ყველა გვერდი ტოლია სიგრძით. ამრიგად, კვადრატისთვის, რომლის გვერდიც ტოლია a-ს, ფართობი განისაზღვრება შემდეგნაირად.
დავიწყოთ მართკუთხა სამკუთხედით, რომელზეც ავაშენეთ კვადრატები ორ მხარეს, ერთი წითელი და ერთი ლურჯი. ჩვენ ვაპირებთ დავშალოთ ამ ორი კვადრატის ნაწილაკები და გადავიტანოთ ისინი ნაცრისფერ კვადრატულ არეში ჰიპოტენუზაზე. ოპერაციის დროს მასალა არ დაგვიკარგავს. ასე რომ, თუ შეგვიძლია ზუსტად შევავსოთ ჰიპოტენუზის კვადრატი, ვაჩვენეთ, რომ ფართობები ტოლია.
როგორ ავაშენოთ კუთხე 45, 30 და 60 გრადუსი
რა თქმა უნდა, ეგვიპტური სამკუთხედი და მისი თვისებები ძალიან სასარგებლოა სახლის აშენებისას. მაგრამ თქვენ მაინც ვერ შეძლებთ სხვა კუთხეების გარეშე. 45 გრადუსიანი კუთხის მისაღებად აიღეთ ჩარჩო ან ბაგეტის მასალა. შემდეგ გაჭერით ორმოცდახუთი გრადუსიანი კუთხით და შეაერთეთ ნახევრები ერთმანეთს.
Რას აკეთებს? პირველი ნაბიჯი აბრუნებს სამკუთხედს ქვემოთ ლურჯ კვადრატზე. ეს ჭრის ლურჯ კვადრატს სამ ნაწილად, ორ სამკუთხედად და წითელ მართკუთხედად. ორი სამკუთხედი ზუსტად იგივე ზომისაა, როგორც თავდაპირველი სამკუთხედი. თავდაპირველი სამკუთხედის "ქვედა" ზუსტად შეესაბამება კვადრატის ვერტიკალურ მხარეს, ვინაიდან კვადრატის გვერდები ტოლია. წითელ მართკუთხედს აქვს მისი ვერტიკალური გვერდები თავდაპირველი სამკუთხედის ფუძის ტოლი, ხოლო მისი ჰორიზონტალური გვერდები უდრის ორიგინალური სამკუთხედის "ქვედა" და "ვერტიკალურ" მხარეს შორის სხვაობას.
Მნიშვნელოვანი ! სასურველი ფერდობის მისაღებად, ამოიღეთ ქაღალდის ნაჭერი ჟურნალიდან და მოხარეთ. ამ შემთხვევაში, მოსახვევის ხაზები გაივლის კუთხეში. კიდეები უნდა ემთხვეოდეს.
როგორც ხედავთ, ფიგურის თვისებები ბევრად აადვილებს და აჩქარებს გეომეტრიული კონსტრუქციის აგებას. 60 გრადუსიანი თანაფარდობის მისაღწევად, თქვენ უნდა აიღოთ ერთი სამკუთხედი 30º-ზე და მეორე იგივე. როგორც წესი, ასეთი პროპორციები აუცილებელია გარკვეული დეკორატიული ელემენტების შექმნისას.
ამ გვერდის ზედა სურათის ტერმინოლოგიის გამოყენებით, წითელი მართკუთხედის ზომები. შემდეგი ნაბიჯი არის წითელი მართკუთხედის გადატანა წითელ მოედანზე. მართკუთხედი წითელ კვადრატს ზემოდან ეკვრის, ხოლო ორი სამკუთხედი რჩება ლურჯ კვადრატზე. შემდეგი ნაბიჯი არის ერთ-ერთი ლურჯი სამკუთხედის ვერტიკალურად გადატანა ჰიპოტენუზის კვადრატზე. ის ზუსტად ემთხვევა ჰიპოტენუზის კვადრატის მხარეს, რადგან კვადრატის გვერდები ტოლია. შემდეგი ნაბიჯი არის მეორე ლურჯი სამკუთხედის გადატანა ჰიპოტენუზის კვადრატში.
შემდეგი ნაბიჯი არის ორიგინალური სამკუთხედის ფორმის კოპირება მარცხნივ წითელ არეში. სამკუთხედი წითელ უბანს ჭრის სამ ნაწილად, ორ სამკუთხედად და პატარა ყვითელ კვადრატად. ორიგინალური სამკუთხედი ზუსტად ერგება ამ რეგიონს ორი მიზეზის გამო; ვერტიკალური გვერდები იდენტურია, ხოლო წითელი უბნის ჰორიზონტალური მხარე უდრის წითელი კვადრატის სიგრძეს პლუს წითელი ოთხკუთხედის ჰორიზონტალური სიგრძე, რომელიც ჩვენ გადავიტანეთ. წითელი ზონის ჰორიზონტალური სიგრძე.
ყურადღება! ექვსკუთხედების შესაქმნელად საჭიროა 30º ასპექტის თანაფარდობა. მათი თვისებები მოთხოვნადია სადურგლო ბლანკებში.
შედეგები

ეგვიპტური სამკუთხედის თვისებები ფართოდ გამოიყენება მშენებლობაში თითქმის ორნახევარი საუკუნის განმავლობაში. ახლაც, ხელსაწყოების ნაკლებობის გამო, მშენებლები იყენებენ პითაგორას მიერ აღმოჩენილ ამ ტექნიკას, რათა მიაღწიონ თუნდაც სწორი კუთხით.

