כל מי שהקשיב בתשומת לב למורה לגיאומטריה בבית הספר מכיר היטב מהו המשולש המצרי. הוא נבדל מסוגים אחרים של דומים עם זווית של 90 מעלות על ידי יחס רוחב-גובה מיוחד. כאשר אדם שומע לראשונה את הביטוי "משולש מצרי", עולות בראשו תמונות של פירמידות מלכותיות ופרעונים. ומה אומרת ההיסטוריה?
מומחים בגיאומטריה מצרית כונו "ארפדונפטי", אלו הקושרים חבלים. על ידי הידוק החבלים שרטו את שני הקווים הפשוטים והחשובים ביותר בגיאומטריה: הקו הישר והעיגול. ראשית, פשוט על ידי הידוק חבל בין שתי נקודות, מעין פעולה שעדיין מתוארת בביטויים "לצייר קו", "לצייר מאונך"; השנייה היא על ידי סיבוב אחת משתי הנקודות סביב השנייה, המוחזקת קבועה. האם הם יכולים לדמיין את מידת ההתפתחות של שתי הפרקטיקות היסודיות הללו?
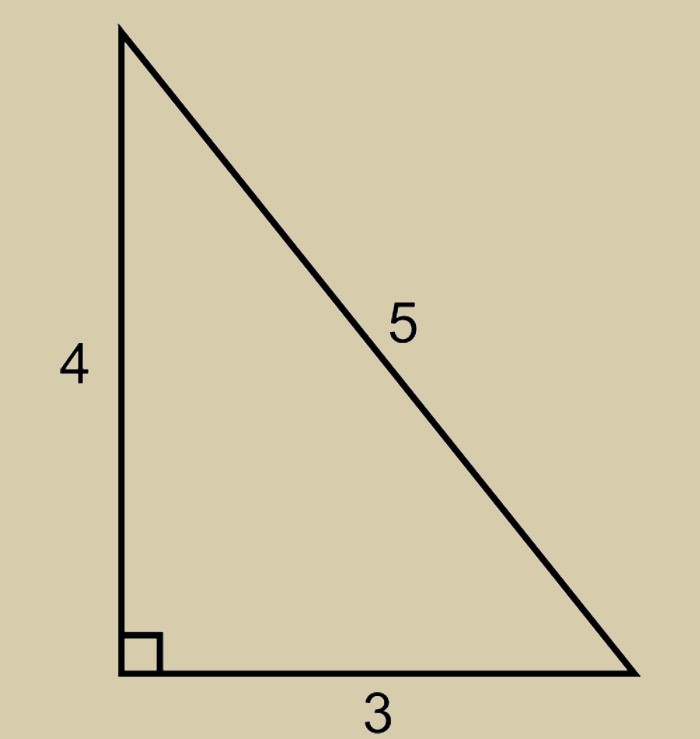
כמו תמיד, קיימות מספר תיאוריות לגבי השם "משולש מצרי". לפי אחד מהם, משפט פיתגורס הידוע ראה את האור דווקא בגלל הדמות הזו. בשנת 535 לפני הספירה. פיתגורס, בעקבות המלצתו של תאלס, נסע למצרים על מנת להשלים כמה פערים בידע במתמטיקה ובאסטרונומיה. שם הוא הפנה את תשומת הלב למוזרויות עבודתם של מודדים מצרים. הם מאוד בצורה יוצאת דופןביצע את הבנייה בזווית ישרה, שצלעותיה היו מחוברות זו לזו ביחס של 3-4-5. סדרה מתמטית זו הקלה יחסית על חיבור הריבועים של כל שלוש הצלעות עם כלל אחד. כך עלה המשפט המפורסם. והמשולש המצרי הוא בדיוק אותה דמות שהניעה את פיתגורס לעשות זאת פתרון מבריק. על פי נתונים היסטוריים אחרים, היוונים נתנו את השם לדמות: באותה תקופה הם ביקרו לעתים קרובות במצרים, שם יכלו להתעניין בעבודתם של מודדי קרקע. יש אפשרות שכמו שקורה לעתים קרובות עם גילויים מדעיים, שני הסיפורים התרחשו בו זמנית, כך שאי אפשר לומר בוודאות מי המציא לראשונה את השם "משולש מצרי". המאפיינים שלו מדהימים וכמובן, אינם מוגבלים ליחס הגובה-רוחב בלבד. השטח והצלעות שלו מיוצגים במספרים שלמים. בשל כך, היישום של משפט פיתגורס עליו מאפשר לנו לקבל מספרים שלמים של ריבועים של תחתית הזרוע והרגליים: 9-16-25. כמובן, זה יכול להיות רק צירוף מקרים. אבל איך, אם כן, להסביר את העובדה שהמצרים ראו במשולש "שלהם" קדוש? הם האמינו בחיבור שלו עם היקום כולו.
למעשה, ייתכן שבקרוב הצרכים המעשיים של מודדים קדומים הולידו את הצורך בעבודות כאלה, שכיום אנו מכנים "ריבוע ומצפן", והכי נכון לכנותן "מעגלים וקווים ישרים". כעת טבעי להתייחס לנייר כזירה הטבעית של הגיאומטריה, כדי שנבין את השימוש בריבועים ומצפנים בלבד, כגבול שרירותי המוטל על ידי רוחות ספקולטיביות שהעדיפו כמה מספרים של אקסיומות על פני שפע של נוחות הנובעת מה שפע של מכשירים.
מכאן ההבדל בין מומחה בגיאומטריה תיאורטית. לפיכך, אנו נוטים להתעלם לחלוטין מהגיאומטריה "בשטח" לטובת ה"על הנייר" הזה, שלא מאפשר לנו להבין שכאשר מעבירים פעולות גיאומטריות מהשדה לנייר, הן ידרשו לעיתים לחלוטין שיטות שונותושיטות.
לאחר שמידע על דמות גיאומטרית יוצאת דופן זו התפרסם, העולם החל לחפש משולשים דומים אחרים עם צלעות שלמות. היה ברור שהם קיימים. אבל חשיבות השאלה לא הייתה רק לבצע חישובים מתמטיים, אלא לבדוק את המאפיינים ה"קדושים". המצרים, על אף חריגותם, מעולם לא נחשבו טיפשים - מדענים עדיין לא יכולים להסביר איך בדיוק נבנו הפירמידות. והנה, פתאום, יוחס לדמות רגילה קשר עם הטבע והיקום. ואכן, כתב היתדות שנמצא מכיל אינדיקציות של כמו משולשעם צד שגודלה מתואר במספר בן 15 ספרות. נכון לעכשיו, המשולש המצרי, שזוויותיו הן 90 (ימין), 53 ו-37 מעלות, נמצא במקומות בלתי צפויים לחלוטין. למשל, כאשר חקרו את התנהגות מולקולות מים רגילות, התברר שהשינוי מלווה בשינוי מבנה של התצורה המרחבית של מולקולות, שבהן ניתן לראות... אותו משולש מצרי. אם נזכור שהוא מורכב משלושה אטומים, אז נוכל לדבר על שלושה צדדים מותנים. כמובן, אנחנו לא מדברים על צירוף המקרים המוחלט של היחס המפורסם, אבל המספרים המתקבלים מאוד מאוד קרובים לאלה הרצויים. האם זה בגלל שהמצרים הכירו במשולש "3-4-5" שלהם כמפתח סמלי ל תופעת טבעוסודות היקום? אחרי הכל, מים, כידוע, הם הבסיס לחיים. ללא ספק, עדיין מוקדם מדי לשים קץ לחקר הדמות המצרית המפורסמת. המדע לעולם אינו ממהר להסיק מסקנות, ומבקש להוכיח את הנחותיו. ולנו נותר רק לחכות ולהיות מופתעים מהידע
אל לנו לשכוח שהדיוק של התוכנית חשוב הרבה יותר מאשר על הנייר. אדריכל שיש לו מושג ברור על התכנית הכוללת ואשר זוכר את התהליך שעבר על מנת לעבור אותה, יזדקק לפרויקט. עדכניות יחסית, כמו גם מפות ישנות, שצוירו בהכרח בכלים ותמיכות ראשוניות, אינן משחזרות את גבולותיה של חלקת אדמה במדויק. למעשה, זה בלתי אפשרי, כי אפילו טעות בנקודת האחוז - הקטנה ביותר שיכולה להתרחש בקנה מידה גדול מספיק - תיצור שגיאה מוחלטת שבקושי יכלה להתקבל בשטח.
המשולש המצרי ותכונותיו ידועות מאז ימי קדם. נתון זה היה בשימוש נרחב בבנייה לסימון ובניית הזוויות הנכונות.
היסטוריה של המשולש המצרי
היוצר של הבנייה הגיאומטרית הזו הוא אחד מגדולי המתמטיקאים של העת העתיקה, פיתגורס. הודות למחקר המתמטי שלו אנו יכולים להשתמש במלוא המאפיינים של הבנייה הגיאומטרית הזו בבנייה.
במקרה זה, הידע על הצורה והמידה של האובייקט המתואר הוא בסיסי; זה לא יהיה תלוי בגיאומטריסט לשחזר בשטח את הדיוק החסר על הנייר. אותו דבר קורה למתמטיקאי, שלא יזדקק כלל לדיוק הקריאות בהדגמות. הגיאומטריה על הנייר מחליפה את דיוק הפעולות בשטח בגיאומטריה של התהליך המנטלי.
להיפך, מהיגיון לדיוק החומרי, כתוצאה מהרחבת קנה המידה הדרושה כדי לעבור מהתוכנית ליצירתה בפועל, פעולת הידוק החבל נותרה אחת הפעולות העיקריות, שכן עד מצרים העתיקה ו. יוון העתיקה. נוהג זה נותר ללא שינוי עד היום, רק עבר על ידי המצאה ושיפור של מכשירים אופטיים מסוימים. למרות שזה די קל לצייר מאונך על נייר עם סרגלים ומרובעים, אותה פעולה על המגרש באותה מידה של דיוק דורשת שיטות שונות בתכלית.
ניתן להניח שמיומנויות מתמטיות אפשרו לפיתגורס להבחין בתבנית בצורות המבנה. פיתוח עתידיניתן בקלות לדמיין אירועים. ניתוח בסיסי והסקת מסקנות יצרו את אחת הדמויות המשמעותיות בהיסטוריה. סביר להניח, הפירמידה של צ'אופס נבחרה כאב טיפוס בגלל הפרופורציות הכמעט מושלמות שלה.
בשטח הריבוע חסר תועלת כי הוא קטן מדי ביחס לגודל הטפסים. גם אם הריבוע מדויק ביותר, האנך שהוא יכול לצייר יגיע למטר הגדול ביותר או הקטן ביותר שלו. אם צריך לסמן ריבוע של 30 מטר לכל צד, עלינו להאריך את הקו הזה 30 פעמים. זו תהיה פעולה כל כך לא מדויקת שהיא כנראה תוביל לאותן תוצאות כאילו מודדים את הזווית הנכונה בערך.
השתקפויות אלו מחזירות אותנו לשאלה המקורית: באילו שיטות השתמשו מודדים מצריים כדי לצייר פיסת אדמה מרובעת? איך הם קיבלו את הפינה המרובעת? אז אם נמתח חבל טבעת באורך 12 יחידות, המסומן בשלוש נקודות במרחקים 3, 4 ו-5, כמשולש עם קודקוד בנקודות המסומנות, הזווית בין הצלעות הקצרות ביותר של המשולש היא זווית ישרה.
משולש מצרי בבנייה
המאפיינים של המבנה הגיאומטרי הייחודי הזה הם שבנייתו ללא שימוש בכלים מאפשרת לבנות בית עם הזוויות הנכונות מכל הבחינות.
חָשׁוּב! כמובן, באופן אידיאלי, האפשרות הטובה ביותר תהיה להשתמש במד זווית או בריבוע.
לא ידוע אם תהליך זה נעשה על ידי אנשי האדמה הקדמונים בזמן אחד, שכן לא הוכח שהמצרים הקדמונים ידעו שמשולש עם הצלעות 3, 4 ו-5 הוא משולש ישר זווית. גם אם הם יודעים על משולש פיתגורי זה או אחר, זה בהכרח אומר שהם הכירו את הטבע, או לפחות איך ליצור את הזווית הישרה.
מאיפה הגיע הידע הזה? בשל היעדר תיעוד ועדים אפילו חלקיים, נוכל לנסות לגשת לבעיה מנקודת מבט שונה, מתמטית ולא היסטורית. השאלה שעלינו לשאול היא מה מייחד את הזווית הנכונה מאחרות? או יותר טוב, מהי התכונה של הזווית של משולש עם הצלעות 3, 4 ו-5?
אז, התכונות של המשולש המצרי מאפשרות לך ליצור את הזוויות הנכונות בכל הפרופורציות. לדפנות המבנה יש את היחס הבא זה לזה:
כדי לבדוק אם ציירתם את הדמות הנכונה, השתמשו במשפט פיתגורס הידוע מבית הספר.
תשומת הלב ! המאפיינים של המשולש המצרי הם כאלה שריבוע התחתון שווה לריבועים של שתי הרגליים.
תשובה מיידית: בניגוד למשולשים אחרים, ניתן לגרום לפיתגורס והפשוטים ביותר, עם הצלעות 3, 4 ו-5, להצטרף אליהם בצד אחד ואז שוב בצד השני. בדרך זו מתקבלת תצורה סימטרית שממלאת את הכל לחלוטין מקום פנויללא חפיפה או פערים.
לאף זווית אחרת מלבד זו הימנית אין את המאפיין הסימטרי הזה, שהופכת להגדרה משלה בספר הגיאומטריה השלם הראשון שהגיע אי פעם לזמננו, היסודות של אוקלידס. כאשר נוצר קו ישר הנופל על אחר זוויות שוות, הם נכונים.
להבנה טובה יותר, בואו ניקח את התלות שלעיל ונחבר דוגמה קטנה. בוא נכפיל חמש בחמש. כתוצאה מכך, נקבל את התחתון השווה ל-25. בוא נחשב את הריבועים של שתי הרגליים. הם יהיו בני 16 ו-9. בהתאם, הסכום שלהם יהיה עשרים וחמש.
לכן המאפיינים של המשולש המצרי משמשים לעתים קרובות כל כך בבנייה. אתה רק צריך לקחת את חומר העבודה ולצייר קו ישר. האורך שלו תמיד צריך להיות כפולה של 5. אז אתה צריך לשרטט קצה אחד ולמדוד ממנו קו שהוא כפולה של 4, ומהשני 3.
טבעה של זווית מרובעת הוא שהזוויות הנובעות מחיתוך שני קווים שוות. ניתן להדגים זאת מיד על הנייר על ידי קיפול הנייר לאורך אחד הקווים המתכנסים ובדיקה שהקו השני מתקפל לבד.
למאפיין זה יש את הבנייה הגיאומטרית ה"קלאסית" של סימון שני עיגולים ואז חיבור הצמתים שלהם. האופי הסימטרי של הצורה ברור למדי, וזו הוכחה ברורה לשוויון הזוויות. יתרה מכך, בניגוד למשולש הפיתגורי, שזקוק לבנייה נוספת, במקרה זה הצורה מציעה מיד את ההגדרה של זווית מרובעת דרך שוויון הזוויות ובו בזמן, בונה את עצמה.
תשומת הלב ! אורך כל קטע יהיה 4 ו-3 ס"מ (בערכי מינימום). החיתוך של קווים אלה יוצר זווית ישרה השווה ל-90 מעלות.
דרכים חלופיות לבניית זווית ישרה של 90 מעלות
כמוזכר לעיל, האופציה הטובה ביותרזה יהיה קל לקחת ריבוע או מד זווית. הכלים הללו מאפשרים העלות הנמוכה ביותרזמן ומאמץ להשיג את הפרופורציות הרצויות. המאפיין העיקרי של המשולש המצרי הוא הרבגוניות שלו. ניתן לבנות דמות מבלי שיהיה כמעט כלום בארסנל.
אלו עדיין רק ניחושים. ללא ספק, תהליך זה בהחלט קל ומדויק יותר מהראשון. ניתן לומר שאנו יכולים לסמן רק את האנך העובר במרכזו של קטע נתון, הנקרא גם ציר הקטע. עם זאת, קל לראות שאם אנו רוצים מאונך בקצה אחד, כמו במקרה של ציור ריבוע, עלינו להכפיל את הקטע, להרחיב אותו למקום בו אנו רוצים לצייר את האנך, ולאחר מכן לחזור על התהליך הקודם. .
יש לציין שכל השיטות הללו מתאימות במיוחד לאדמות מישוריות כמו מישור מצרים. כדי להבין טוב יותר כמה מהבעיות הקשורות למטוסים ולמנועים, יש צורך להשתמש בכמה רעיונות מתמטיים מהטריגונומטריה כדי ללמוד משולשים. נתחיל עם כמה הגדרות ומינוחים שבהם נשתמש בשקופית זו. בוא נתחיל עם משולש ישר זווית. המשולש הימני הוא דמות תלת-תדרלית עם זווית אחת השווה ל-90 מעלות.
חזק בבנייה זווית נכונהמהדורות מודפסות פשוטות עוזרות. קח כל מגזין או ספר. העובדה היא שאצלם יחס הגובה-רוחב הוא תמיד בדיוק 90 מעלות. מכונות דפוס פועלות בצורה מדויקת מאוד. אחרת, הגליל שיוזן למכונה ייחתך עם פינות עקומות לא פרופורציונליות.
זווית של 90 מעלות נקראת זווית ישרה, ומכאן קיבל המשולש הימני את שמו. זוהי הצלע הארוכה ביותר מבין שלוש הצלעות של המשולש הישר זווית. המילה "היפוטנוז" מגיעה משתי מילים יווניות שמשמעותן "למתוח" מכיוון שהיא הצד הארוך ביותר.
משפט פיתגורס הוא משפט המקשר את אורכי הצלעות של כל משולש ישר זווית. עבור כל משולש ישר זווית, ריבוע התחתון. שווה לסכום הריבועים של שתי הצלעות האחרות. זה כתוב מתמטית. משפט זה היה ידוע בתרבויות רבות בשמות רבים במהלך השנים. מאמינים שהוא למד את המשפט בזמן שלמד במצרים. המצרים כנראה ידעו על מערכות יחסים אלף שנים לפני פיתגורס.
איך להשיג משולש מצרי עם חבל

מאפיינים של זה דמות גיאומטריתקשה להעריך יתר על המידה. אין זה מפתיע שמהנדסי העת העתיקה מצאו דרכים רבות ליצור אותו תוך שימוש במשאבים מינימליים.
אחת הפשוטות היא שיטת יצירת המשולש המצרי על כל תכונותיו הנובעות מכך באמצעות חבל פשוט. קח את החוט וחתך אותו ל-12 חתיכות אחידות לחלוטין. מהם, הוסף דמות עם פרופורציות של 3, 4 ו-5.
פיתגורס הכליל את התוצאה לכל משולש ישר זווית. ישנן הוכחות אלגבריות וגאומטריות רבות ושונות למשפט. רובם מתחילים בבניית ריבועים על שרטוט של המשולש הימני הראשי. בציור בראש עמוד זה, אנו מציגים ריבועים מצוירים בשלושת צלעותיו של משולש. ריבוע הוא מקרה מיוחד של מלבן שבו כל הצלעות שוות באורכן. לפיכך, עבור ריבוע עם צלע שווה ל-a, השטח נקבע באופן הבא.
נתחיל במשולש הימני, עליו בנינו ריבועים משני צדדים, אחד אדום ואחד כחול. אנחנו הולכים לפרק את החלקים של שני הריבועים האלה ולהעביר אותם לאזור של הריבוע האפור על התחתון. לא איבדנו שום חומר במהלך המבצע. אז אם נוכל למלא במדויק את הריבוע של התחתון, הראינו שהשטחים שווים.
איך לצייר זווית של 45, 30 ו-60 מעלות
כמובן שהמשולש המצרי ותכונותיו שימושיים מאוד בבניית בית. אבל בלי זוויות אחרות אתה עדיין לא יכול לעשות. כדי לקבל זווית שווה ל-45 מעלות, קח את החומר של המסגרת או הבאגט. אחר כך ראו אותו בזווית של ארבעים וחמש מעלות ועגנו את החצאים אחד עם השני.
מה הוא עושה? הצעד הראשון מסובב את המשולש מטה לריבוע כחול. זה חותך את הריבוע הכחול לשלושה חלקים, שני משולשים ומלבן אדום. שני המשולשים באותו גודל בדיוק כמו המשולש המקורי. ה"תחתית" של המשולש המקורי מתאימה בדיוק לצלע האנכית של הריבוע, שכן צלעות הריבוע שוות. למלבן האדום צלעותיו האנכיות שוות לבסיס המשולש המקורי, והצלעות האופקיות שלו שוות להפרש בין הצלע ה"תחתונה" לצלע ה"אנכית" של המשולש המקורי.
חשוב! כדי לקבל את השיפוע הרצוי, תלשו פיסת נייר מהמגזין וקפלו אותה. במקרה זה, קווי העיקול יעברו דרך הפינה. הקצוות חייבים להתאים.
כפי שאתה יכול לראות, מאפייני הצורה הופכים את זה הרבה יותר קל ומהיר לבנות מבנה גיאומטרי. כדי להשיג יחס רוחב-גובה של 60 מעלות, עליך לקחת משולש אחד ב-30º והשני זהה. בדרך כלל, פרופורציות כאלה נחוצות בעת יצירת אלמנטים דקורטיביים מסוימים.
בעזרת המינוח מהאיור בראש עמוד זה, מידות המלבן האדום. השלב הבא הוא להעביר את המלבן האדום על הריבוע האדום. המלבן בולט על גבי הריבוע האדום, בעוד שני המשולשים נשארים על הריבוע הכחול. השלב הבא הוא להעביר את אחד המשולשים הכחולים בצורה אנכית לתוך ריבוע ההיפוטנוז. זה מתאים בדיוק לצלע הריבוע של התחתון כי צלעות הריבוע שוות. השלב הבא הוא להזיז את המשולש הכחול השני לריבוע התחתון.
השלב הבא הוא להעתיק את צורת המשולש המקורי שמאלה לאזור האדום. המשולש חותך את האזור האדום לשלושה חלקים, שני משולשים וריבוע צהוב קטן. המשולש המקורי מתאים בדיוק לאזור זה משתי סיבות; הצלעות האנכיות זהות, והצד האופקי של השטח האדום הוא אורך הריבוע האדום בתוספת האורך האופקי של המלבן האדום שהזזנו. האורך האופקי של האזור האדום.
תשומת הלב ! יש צורך ביחס רוחב-גובה של 30º כדי ליצור משושים. הנכסים שלהם מבוקשים בחסרי נגרות.
תוצאות

המאפיינים של המשולש המצרי נמצאים בשימוש נרחב בבנייה במשך כמעט מאתיים וחצי. אפילו עכשיו, עם מחסור בכלים, בונים משתמשים בטכניקה הזו שגילה פיתגורס כדי להשיג זוויות ישרות אפילו.

