Everyone who listened attentively to a geometry teacher at school is very familiar with what the Egyptian triangle is. It differs from other types of similar ones with an angle of 90 degrees by a special aspect ratio. When a person first hears the phrase "Egyptian triangle", pictures of majestic pyramids and pharaohs come to mind. And what does history say?
Experts in Egyptian geometry were called "arpedonapti", those who tie ropes. It was by tightening the ropes that they drew the two simplest and most important lines in geometry: the straight line and the circle. First, by simply tightening a rope between two points, a kind of operation that is still depicted in the expressions "draw a line", "draw a perpendicular"; The second is by making one of the two points rotate around the other, which is held fixed. Can they imagine the degree of development of these two elementary practices?
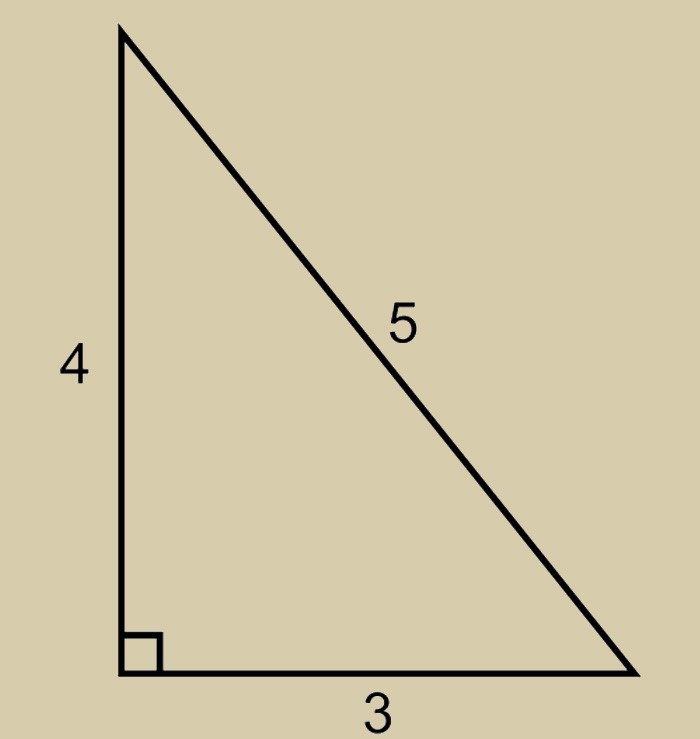
As is always the case, there are several theories regarding the name "Egyptian triangle". According to one of them, the well-known Pythagorean theorem saw the light precisely because of this figure. In 535 BC. Pythagoras, following the recommendation of Thales, went to Egypt in order to fill in some gaps in the knowledge of mathematics and astronomy. There he drew attention to the peculiarities of the work of Egyptian surveyors. They are very in an unusual way performed the construction with a right angle, the sides of which were interconnected with one another by a ratio of 3-4-5. This mathematical series made it relatively easy to connect the squares of all three sides with one rule. This is how the famous theorem arose. And the Egyptian triangle is precisely the same figure that prompted Pythagoras to brilliant solution. According to other historical data, the Greeks gave the name to the figure: at that time they often visited Egypt, where they could be interested in the work of land surveyors. There is a possibility that, as is often the case with scientific discoveries, both stories happened at the same time, so it’s impossible to say with certainty who first came up with the name “Egyptian triangle”. Its properties are amazing and, of course, are not limited to the aspect ratio alone. Its area and sides are represented by whole numbers. Due to this, the application of the Pythagorean theorem to it allows us to obtain integer numbers of squares of the hypotenuse and legs: 9-16-25. Of course, this could just be a coincidence. But how, then, to explain the fact that the Egyptians considered "their" triangle sacred? They believed in its interconnection with the entire universe.
In fact, the practical needs of ancient surveyors may soon have given rise to the need for such works, which today we call "square and compass", and these should most correctly be called "circles and straight lines". It is now natural to regard paper as the natural arena of geometry, so that we understand the use of squares and compasses alone, as an arbitrary limit imposed by speculative spirits who have preferred a few numbers of axioms to a multitude of conveniences deriving from the multitude of instruments.
Hence the difference between an expert in theoretical geometry. Thus, we tend to ignore completely the geometry "in the field" in favor of this "on paper", which does not allow us to understand that when transferring geometric operations from the field to paper, they will sometimes require completely different methods and methods.
After information about this unusual geometric figure became public, the world began searching for other similar triangles with integer sides. It was obvious that they existed. But the importance of the question was not just to perform mathematical calculations, but to test the "sacred" properties. The Egyptians, for all their unusualness, were never considered stupid - scientists still cannot explain exactly how the pyramids were built. And here, suddenly, a connection with Nature and the Universe was attributed to an ordinary figure. Indeed, the found cuneiform contains indications of like a triangle with a side whose size is described by a 15-digit number. Currently, the Egyptian triangle, the angles of which are 90 (right), 53 and 37 degrees, are found in completely unexpected places. For example, when studying the behavior of ordinary water molecules, it turned out that the change is accompanied by a restructuring of the spatial configuration of molecules, in which one can see ... the same Egyptian triangle. If we remember that it consists of three atoms, then we can talk about conditional three sides. Of course, we are not talking about the complete coincidence of the famous ratio, but the resulting numbers are very, very close to the desired ones. Is it because the Egyptians recognized their "3-4-5" triangle as a symbolic key to natural phenomena and the secrets of the universe? After all, water, as you know, is the basis of life. Without a doubt, it is still too early to put an end to the study of the famous Egyptian figure. Science never rushes to conclusions, seeking to prove its assumptions. And we can only wait and be surprised by the knowledge
We should not forget that the accuracy of the plan is much more important than on paper. An architect who has a clear idea of the overall plan and who remembers the process he went through in order to go through it would need a blueprint. Relatively recent, as well as old maps, which were inevitably drawn with rudimentary tools and supports, do not reproduce the boundaries of a piece of land accurately. In fact, this is impossible, because even a percentage point error - the smallest that can occur on a sufficiently large scale - would generate an absolute error that could hardly be accepted on the field.
The Egyptian triangle and its properties have been well known since ancient times. This figure was widely used in construction for marking and building the right angles.
History of the Egyptian Triangle
The creator of this geometric construction is one of the greatest mathematicians of antiquity, Pythagoras. It is thanks to his mathematical research that we can fully use all the properties of this geometric construction in construction.
In this case, knowledge of the shape and measure of the object to be described is fundamental; it will not be up to the geometrist to reproduce in the field the precision missing on paper. The same thing happens to the mathematician, who will not need the accuracy of the readings at all in demonstrations. The geometry on paper replaces the accuracy of operations on the field with the geometry of the mental process.
On the contrary, from logic to material accuracy, as a consequence of the necessary expansion of the scale to move from the plan to the actual creation of it, the act of tightening the rope remained one of the main operations, since until Ancient Egypt and Ancient Greece. This practice has remained unchanged until the present, only passed down by the invention and improvement of certain optical instruments. Although it is quite easy to draw a perpendicular on paper with rulers and squares, the same operation on the field with the same degree of accuracy requires radically different methods.
It can be assumed that mathematical skills allowed Pythagoras to notice a pattern in the forms of the structure. Further development events can be easily imagined. Basic analysis and drawing conclusions created one of the most significant figures in history. Most likely, the pyramid of Cheops was chosen as a prototype because of its almost perfect proportions.
In the field, the square is useless because it is too small in relation to the size of the forms. Even if the square is extremely precise, the perpendicular it can draw will reach its largest or smallest meter. If we need to mark a square of 30 meters per side, we must extend this line 30 times. This would be such an imprecise operation that it would probably lead to the same results as if we measured the correct angle approximately.
These reflections bring us back to the original question: What methods were used by Egyptian measurers to draw a square piece of land? How did they get the square corner? So if we stretch a ring rope 12 units long, marked at three points at distances 3, 4 and 5, as a triangle with apex at the marked points, the angle between the shortest sides of the triangle is a right angle.
Egyptian triangle in construction
The properties of this unique geometric structure are that its construction without the use of any tools allows you to build a house with the correct angles in all respects.
Important! Of course, ideally, the best option would be to use a protractor or square.
It is not known whether this process was done by the ancient earthmen at one time, as it is not proven that the ancient Egyptians knew that a triangle with sides 3, 4, and 5 is a right triangle. Even if they know about this or other Pythagorean triangles, it necessarily means that they knew the nature, or at least how to create the right angle.
Where did this knowledge come from? Due to the lack of even partial documentation and witnesses, we can try to approach the problem from a different point of view, mathematical rather than historical. The question we have to ask is what makes the right angle different from others? Or better, what is the feature of the angle of a triangle with sides 3, 4, and 5?
So, the qualities of the Egyptian triangle allow you to make the right angles in all proportions. The sides of the structure have the following relationship to each other:
To check whether you have drawn the right figure, use the well-known Pythagorean Theorem from school.
Attention ! The properties of the Egyptian triangle are such that the square of the hypotenuse is equal to the squares of the two legs.
Immediate answer: unlike other triangles, the Pythagorean and most simple ones, with sides 3, 4 and 5, can be made to join them on one side and then again on the other. In this way, a symmetrical configuration is obtained that completely fills all free space no overlap or gaps.
No other angle but the right one has this symmetrical characteristic, which becomes its own definition in the first complete book of geometry that has ever reached our time, Euclid's Elements. When a straight line falling on another forms equal angles, they are correct.
For a better understanding, let's take the above dependence and compose small example. Let's multiply five by five. As a result, we get the hypotenuse equal to 25. Let's calculate the squares of the two legs. They will be 16 and 9. Accordingly, their sum will be twenty-five.
That is why the properties of the Egyptian triangle are so often used in construction. You just need to take the workpiece and draw a straight line. Its length should always be a multiple of 5. Then you need to outline one edge and measure a line from it that is a multiple of 4, and from the second 3.
The nature of a square angle is that the angles resulting from the intersection of two lines are equal. This can be immediately demonstrated on paper by folding the paper along one of the converging lines and checking that the other line folds on its own.
This property has the "classical" geometric construction of marking two circles and then joining their intersections. The symmetrical character of the form is quite obvious, and this is a clear proof of the equality of the angles. Moreover, unlike the Pythagorean triangle, which needs further construction, in this case the form immediately offers the definition of a square angle through the equality of angles and at the same time, builds itself.
Attention ! The length of each segment will be 4 and 3 cm (at minimum values). The intersection of these lines forms a right angle equal to 90 degrees.
Alternative Ways to Construct a 90 Degree Right Angle
As mentioned above, the best option it will be easy to take a square or a protractor. These tools allow least cost time and effort to achieve the desired proportions. The main property of the Egyptian triangle lies in its versatility. A figure can be built without having practically nothing in the arsenal.
These are still mere guesses. Without a doubt, this process is definitely easier and more accurate than the first one. It can be said that we can only mark the perpendicular passing through the center of a given segment, also called the axis of the segment. However, it is easy to see that if we want a perpendicular on one edge, as in the case of drawing a square, we need to double the segment, extending it to where we want to draw the perpendicular, and then repeat the preceding process.
It should be noted that all these methods are particularly suitable for flat lands such as the Egyptian plain. To better understand some of the problems associated with aircraft and engines, it is necessary to use some mathematical ideas from trigonometry to study triangles. Let's start with some definitions and terminology that we'll be using on this slide. Let's start with right triangle. The right triangle is a trihedral figure with one angle equal to 90 degrees.
Strong in construction right angle simple printed editions help. Take any magazine or book. The fact is that in them the aspect ratio is always exactly 90 degrees. Printing presses work very accurately. Otherwise, the roll that is fed into the machine will be cut with disproportionate curved corners.
An angle of 90 degrees is called a right angle, and this is where the right triangle gets its name. This is the longest side of the three sides of the right triangle. The word "hypotenuse" comes from two Greek words meaning "to stretch" as it is the longest side.
The Pythagorean theorem is a statement relating the lengths of the sides of any right triangle. For any right triangle, the square of the hypotenuse. is equal to the sum of the squares of the other two sides. It's written mathematically. This theorem has been known in many cultures by many names over the years. It is believed that he learned the theorem while studying in Egypt. The Egyptians probably knew about relationships a thousand years before Pythagoras.
How to get an Egyptian triangle with a rope

properties of this geometric figure hard to overestimate. It is not surprising that the engineers of antiquity came up with many ways to form it using minimal resources.
One of the simplest is the method of forming the Egyptian triangle with all its ensuing properties by means of a simple rope. Take the twine and cut it into 12 absolutely even pieces. From them, add a figure with proportions of 3, 4 and 5.
Pythagoras generalized the result to any right triangle. There are many different algebraic and geometric proofs of the theorem. Most of them start by building squares on a sketch of the main right triangle. In the drawing at the top of this page, we show squares drawn on the three sides of a triangle. A square is a special case of a rectangle in which all sides are equal in length. Thus, for a square with a side equal to a, the area is determined as follows.
Let's start with the right triangle, on which we've built squares on two sides, one red and one blue. We are going to break up the pieces of these two squares and move them to the area of the gray square on the hypotenuse. We didn't lose any material during the operation. So if we can exactly fill in the square of the hypotenuse, we have shown that the areas are equal.
How to draw an angle of 45, 30 and 60 degrees
Of course, the Egyptian triangle and its properties are very useful when building a house. But without other angles you still can not do. To get an angle equal to 45 degrees, take the material of the frame or baguette. Then saw it at an angle of forty-five degrees and dock the halves with each other.
What is he doing? The first step rotates the triangle down into a blue square. This cuts the blue square into three pieces, two triangles and a red rectangle. The two triangles are exactly the same size as the original triangle. The "bottom" of the original triangle corresponds exactly to the vertical side of the square, since the sides of the square are equal. The red rectangle has its vertical sides equal to the base of the original triangle, and its horizontal sides are equal to the difference between the "bottom" side and the "vertical" side of the original triangle.
Important ! To get the desired slope, tear a piece of paper out of the magazine and fold it. In this case, the bend lines will pass through the corner. The edges must match.
As you can see, the shape properties make it much easier and faster to build a geometric construct. To achieve an aspect ratio of 60 degrees, you need to take one triangle at 30º and the second is the same. Usually, such proportions are necessary when creating certain decorative elements.
Using the terminology from the figure at the top of this page, the dimensions of the red rectangle. The next step is to move the red rectangle over the red square. The rectangle sticks out on top of the red square, while the two triangles remain on the blue square. The next step is to move one of the blue triangles vertically into the hypotenuse square. It corresponds exactly to the side of the square of the hypotenuse because the sides of the square are equal. The next step is to move the other blue triangle into the hypotenuse square.
The next step is to copy the shape of the original triangle to the left into the red area. The triangle cuts the red area into three pieces, two triangles and a small yellow square. The original triangle corresponds exactly to this region for two reasons; the vertical sides are identical, and the horizontal side of the red area is the length of the red square plus the horizontal length of the red rectangle we moved. The horizontal length of the red area.
Attention ! An aspect ratio of 30º is needed to make hexagons. Their properties are in demand in carpentry blanks.
Results

The properties of the Egyptian triangle have been widely used in construction for almost two and a half centuries. Even now, with a lack of tools, builders use this technique discovered by Pythagoras to achieve even right angles.

